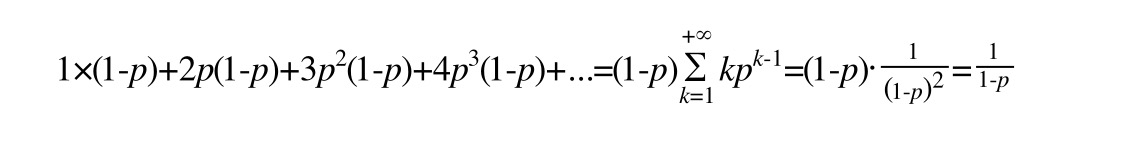Phân tích cấu trúc dữ liệu nội bộ của Redis (6) —— skiplist

2016-10-05

Phân tích cấu trúc dữ liệu nội bộ của Redis Phân tích cấu trúc dữ liệu nội bộ của Redis Bài viết này là phần thứ sá Trong nội dung hôm naytỷ lệ kèo bóng đá trực tiếp, chúng ta sẽ cùng tìm hiểu về một cấu trúc dữ liệu nội bộ của Redis — skiplist. Đây là một phần quan trọng giúp tối ưu hóa hiệu suất và tăng tốc độ truy xuất dữ liệu trong hệ thống Redis.

Trong Rediskeo nha cai hom nay, việc sử dụng danh sách nhảy (skiplist) nhằm mục đích xây dựng cấu trúc dữ liệu bên ngoài được gọi là tập hợp đã sắp xếp (sorted set). Tập hợp đã sắp xếp cung cấp một loạt các thao tác rất đa dạng, có thể đáp ứng nhiều tình huống thực tế khác nhau. Điều này cũng đồng nghĩa với việc việc triển khai tập hợp đã sắp xếp sẽ phức tạp hơn so với các cấu trúc dữ liệu khác. Đồng thời, đối với nhiều người, danh sách nhảy là một khái niệm khá xa lạ, vì hầu hết các trường đại học không đề cập chi tiết về cấu trúc dữ liệu này trong các khóa học về thuật toán. Do đó, để giải thích rõ ràng và dễ hiểu hơn, bài viết này sẽ dành nhiều thời gian hơn so với các phần còn lại của loạt bài này. Danh sách nhảy không chỉ giúp tăng tốc độ truy xuất mà còn cho phép Redis quản lý các phần tử theo thứ tự, tạo điều kiện cho việc tìm kiếm nhanh chóng và linh hoạt. Trong khi đó, việc thiếu kiến thức nền tảng về danh sách nhảy có thể khiến nhiều lập trình viên gặp khó khăn khi hiểu sâu về cách hoạt động của nó. Hiểu rõ bản chất và cơ chế của danh sách nhảy sẽ giúp chúng ta nắm bắt cách Redis tối ưu hóa hiệu suất cho các thao tác liên quan đế Bằng cách đi sâu vào từng khía cạnh của danh sách nhảy, bài viết này hy vọng sẽ giúp độc giả không chỉ hiểu rõ hơn về cách hoạt động của nó mà còn thấy được tầm quan trọng của nó trong việc xây dựng các hệ thống lưu trữ và xử lý dữ liệu hiện đại.

Chúng ta sẽ giới thiệu chi tiết trong ba phần chính sau đây:

1. Hãy cùng tìm hiểu về cấu trúc dữ liệu skiplistkeo nha cai hom nay, một trong những cấu trúc nổi tiếng trong lĩnh vực lập trình. Skiplist là một cách sáng tạo để sắp xếp và truy xuất dữ liệu hiệu quả, với ý tưởng khá đơn giản nhưng đầy tinh tế. Trong phần này, chúng ta sẽ không đề cập đến Redis mà tập trung vào việc giải thích rõ ràng về cách hoạt động củ Cấu trúc skiplist có thể được hình dung như một hệ thống nhiều tầng, trong đó mỗi tầng chứa một số lượng các nút nhất định. Các nút ở tầng trên chỉ bao gồm một số nhỏ hơn của các yếu tố so với tầng dưới, và nhiệm vụ chính của nó là giúp tìm kiếm nhanh hơn. Khi bạn cần tìm kiếm một giá trị cụ thể, thay vì phải duyệt qua toàn bộ danh sách từ đầu đến cuối, bạn chỉ cần di chuyển qua từng tầng cao và giảm phạm vi tìm kiếm một cách hợp lý. Về mặt thuật toán, skiplist hoạt động tương tự như một cây nhị phân cân bằng nhưng với cơ chế ngẫu nhiên hóa. Điều này làm cho việc thêm, xóa hoặc tìm kiếm các phần tử trở nên nhanh chóng và hiệu quả. Cụ thể, độ phức tạp trung bình của các hoạt động này thường nằm ở mức O(log n), điều này rất quan trọng khi bạn cần xử lý một lượng lớn dữ liệu. Hy vọng qua cách giải thích này, bạn đã có thể hình dung rõ hơn về skiplist và cách nó hoạt động. Đây là một công cụ hữu ích trong nhiều ứng dụng khác nhau và không chỉ giới hạn trong Redis hay bất kỳ hệ thống nào. Hãy nhớ rằng, sự linh hoạt và khả năng mở rộng của skiplist khiến nó trở thành một lựa chọn tuyệt vời trong nhiều tình huống thực tế!
2. Trong Redisđá gà trực tiếp app, việc triển khai skiplist cụ thể được thiết kế để đáp ứng các yêu cầu đặc biệt của tập hợp đã sắp xếp (sorted set). So với phiên bản skiplist cổ điển, triển khai trong Redis đã thực hiện một số điều chỉnh đáng kể. Những thay đổi này giúp tối ưu hóa hiệu suất và phù hợp hơn với cấu trúc dữ liệu phức tạp của sorted set, đảm bảo rằng các hoạt động như thêm, xóa hoặc tìm kiếm phần tử đều diễn ra một cách nhanh chóng và hiệu quả. Các điều chỉnh này không chỉ giúp cải thiện khả năng truy xuất mà còn đảm bảo tính ổn định và độ tin cậy cho toàn bộ hệ thống.
3. Bạn có thể tìm hiểu cách sorted set được xây dựng dựa trên sự kết hợp của skiplisttỷ lệ kèo bóng đá trực tiếp, dict và ziplist. Skiplist đóng vai trò như một cấu trúc dữ liệu giúp truy xuất phần tử theo thứ tự nhanh chóng, trong khi dict đảm bảo tốc độ truy vấn và cập nhật bằng cách sử dụ Còn ziplist được sử dụng để lưu trữ các phần tử nhỏ hơn với không gian bộ nhớ tiết kiệm hơn. Ba thành phần này phối hợp nhịp nhàng để tạo ra một sorted set linh hoạt, hiệu quả cả về thời gian lẫn bộ nhớ. Skiplist đảm bảo khả năng tìm kiếm nhanh chóng, dict giúp duy trì tính duy nhất và tốc độ, còn ziplist tối ưu hóa không gian cho những trường hợp dữ liệu nhỏ gọn. Sự kết hợp này đã làm cho sorted set trở thành một trong những tính năng mạnh mẽ nhất của Redis.

Trong quá trình thảo luậnkeo nha cai hom nay, chúng ta sẽ còn đề cập đến hai cấu hình Redis quan trọng (ở phần ADVANCED CONFIG trong tệp redis.conf):

								
									zset-max-ziplist-entries 128
zset-max-ziplist-value 64

								

Trong quá trình thảo luậntỷ lệ kèo bóng đá trực tiếp, chúng tôi sẽ giải thích chi tiết ý nghĩa của hai cấu hình này.

Lưu ý: Việc phân tích mã nguồn trong bài viết này dựa trên nhánh 3.2 của mã nguồn gốc của Redis.

Giới thiệu về cấu trúc dữ liệu skiplist

Skiplist về bản chất cũng là một loại cấu trúc tìm kiếmđá gà trực tiếp app, được thiết kế để giải quyết các vấn đề liên quan đến việc tìm kiếm trong thuật toán (Searching). Cụ thể, dựa trên khóa (key) đã cho trước, skiplist giúp xác định vị trí của nó (hoặc giá trị tương ứng - value) một cách nhanh chóng và hiệu quả. Với cơ chế phân tầng thông minh, skiplist không chỉ tối ưu hóa thời gian tìm kiếm mà còn tạo ra sự cân bằng giữa hiệu suất và độ phức tạp trong xử lý dữ liệu.

Phân tích cấu trúc dữ liệu nội bộ của Redis Phần đầu tiên Trong phần giới thiệu về dictđá gà trực tiếp app, chúng ta đã từng thảo luận rằng các phương pháp giải quyết vấn đề tìm kiếm thường được chia thành hai nhóm lớn: một là dựa trên các cây cân bằng (balanced tree), và hai là dựa trên bảng băm (hash table). Tuy nhiên, skip list lại khá đặc biệt, nó không thể xếp vào bất kỳ nhóm nào trong hai nhóm đó.

Loại cấu trúc dữ liệu này được phát minh bởi William Pugh Ông đã xuất bản bài báo năm 1990 có tiêu đề "<" Skip Lists: A Probabilistic Alternative to Balanced Trees >. Những bạn quan tâm đến chi tiết có thể tải bài báo gốc để đọc.

Skiplisttỷ lệ kèo bóng đá trực tiếp, như tên gọi gợi ý, trước hết là một danh sách (list). Về bản chất, nó được phát triển dựa trên ý tưởng của danh sách liên kết có thứ tự. Tuy nhiên, khác biệt lớn nhất so với danh sách liên kết thông thường là skiplist sử dụng nhiều lớp cấp bậc, mỗi lớp đại diện cho một "mức độ nhảy" (level) trong dữ liệu. Điều này giúp cải thiện đáng kể hiệu suất tìm kiếm, vì thay vì duyệt từng phần tử như trong danh sách liên kết cơ bản, skiplist cho phép bạn "nhảy" qua các phần tử không cần thiết, từ đó rút ngắn thời gian truy xuất dữ liệu.

Trước tiêntỷ lệ kèo bóng đá trực tiếp, hãy xem một danh sách liên kết có thứ tự như dưới đây (nút màu xám ở phía bên trái biểu thị một nút đầu trống):

Trong một danh sách liên kết như vậykeo nha cai hom nay, nếu chúng ta muốn tìm kiếm một giá trị cụ thể, thì phải bắt đầu từ đầu danh sách và so sánh lần lượt từng nút cho đến khi tìm thấy nút chứa giá trị cần tìm hoặc gặp nút có giá trị lớn hơn giá trị được chỉ định (trường hợp không tìm thấy). Điều này có nghĩa là độ phức tạp thời gian sẽ ở mức O(n). Tương tự, khi muốn chèn thêm một giá trị mới vào danh sách, chúng ta cũng cần thực hiện quá trình tìm kiếm tương tự để xác định vị trí thích hợp cho việc chèn đó. Quá trình này đòi hỏi phải duyệt qua nhiều phần tử trong danh sách, khiến hiệu suất của nó phụ thuộc trực tiếp vào số lượng phần tử hiện tại.

Giả sử chúng ta thêm một con trỏ giữa mỗi hai nútkeo nha cai hom nay, cho phép con trỏ chỉ xuống nút tiếp theo, như hình dưới đây:

Chỉ với những con trỏ mới được thêm vàotỷ lệ kèo bóng đá trực tiếp, chúng ta đã tạo thành một danh sách liên kết hoàn toàn mới, nhưng số lượng nút trong danh sách này chỉ bằng một nửa so với danh sách ban đầu (trong hình minh họa là các nút 7, 19 và 26). Hiện tại, khi cần tìm kiếm dữ liệu, chúng ta có thể bắt đầu từ danh sách liên kết mới này. Khi gặp một nút có giá trị lớn hơn giá trị cần tìm, chúng ta sẽ chuyển sang danh sách gốc để tiếp tục tìm kiếm. Ví dụ, nếu muốn tìm kiếm giá trị 23, quá trình tìm kiếm sẽ đi theo hướng mà các con trỏ được đánh dấu đỏ trong hình minh họa chỉ dẫn: từ nút đầu tiên trong danh sách mới, tiến tới nút cần thiết trong danh sách gốc.

• 23 trước tiên so sánh với 7đá gà trực tiếp app, rồi so sánh với 19, lớn hơn cả hai, tiếp tục so sánh tiếp.
• Khi so sánh 23 và 26đá gà trực tiếp app, nó nhỏ hơn 26, do đó trở lại danh sách ban đầu (danh sách liên kết), so sánh với 22.
• Bạn có thể thấy rằng 23 lớn hơn 22tỷ lệ kèo bóng đá trực tiếp, vì vậy hãy tiếp tục di chuyển theo mũi tên bên dưới để so sánh với số tiếp theo là 26. Khi so sánh, bạn sẽ nhận ra rằng 23 nhỏ hơn 26, điều này cho thấy dữ liệu cần tìm (23) không tồn tại trong danh sách liên kết gốc. Đồng thời, vị trí mà nó nên được chèn sẽ nằm giữa 22 và 26, tạo thành một chuỗi sắp xếp hợp lý hơn trong danh sách.

Trong quá trình tìm kiếm nàytỷ lệ kèo bóng đá trực tiếp, nhờ việc bổ sung thêm con trỏ, chúng ta không cần phải so sánh từng bước với tất cả các nút trong danh sách liên kết nữa. Số lượng nút cần so sánh hiện tại chỉ còn khoảng một nửa so với trước đây. Điều này giúp tiết kiệm đáng kể thời gian và công sức thực hiện so sánh, đồng thời cải thiện hiệu suất đáng kể của thuật toán.

Chúng ta có thể áp dụng cách tương tự để tiếp tục thêm các con trỏ vào mỗi cặp nút mới xuất hiện trong chuỗi liên kết cấp trênđá gà trực tiếp app, từ đó tạo ra một chuỗi liên kết thứ ba. Dưới đây là minh họa: Mỗi bước mở rộng này không chỉ giúp tối ưu hóa việc truy xuất dữ liệu mà còn tăng cường khả năng truy cập linh hoạt giữa các nút. Với mỗi lớp mới được bổ sung, cấu trúc dữ liệu trở nên mạnh mẽ hơn, sẵn sàng đối mặt với nhiều tình huống phức tạp hơn trong thực tế.

Trong cấu trúc danh sách liên kết ba lớp nàyđá gà trực tiếp app, nếu chúng ta vẫn đang tìm kiếm số 23, thì đầu tiên theo danh sách lớp trên cùng, chúng ta sẽ so sánh với số 19. Khi nhận thấy rằng 23 lớn hơn 19, điều đó đồng nghĩa với việc chúng ta chỉ cần tiếp tục tìm kiếm ở phía sau số 19 và hoàn toàn có thể bỏ qua tất cả các nút trước đó. Có thể hình dung rằng khi danh sách càng dài, cách tìm kiếm thông qua các lớp danh sách đa tầng này cho phép chúng ta bỏ qua rất nhiều nút ở tầng dưới, từ đó tăng đáng kể tốc độ tìm kiếm. Điều này thực sự là một lợi thế lớn khi làm việc với những tập dữ liệu khổng lồ, giúp tiết kiệm thời gian đáng kể trong quá trình xử lý.

Skiplist được thiết kế dựa trên ý tưởng của danh sách liên kết đa lớp này. Về cơ bảntỷ lệ kèo bóng đá trực tiếp, theo cách tạo danh sách liên kết như đã mô tả ở trên, số lượng các nút ở mỗi lớp trên sẽ bằng một nửa số lượng nút ở lớp dưới cùng, điều này làm cho quá trình tìm kiếm trở nên rất giống với việc thực hiện tìm kiếm nhị phân, từ đó giảm thời gian phức tạp xuống còn O(log n). Tuy nhiên, phương pháp này gặp vấn đề lớn khi chèn dữ liệu. Khi chèn một nút mới vào, mối quan hệ tương ứng 2:1 giữa số lượng nút ở các lớp liền kề sẽ bị phá vỡ. Nếu muốn duy trì mối quan hệ này, tất cả các nút phía sau nút vừa chèn (bao gồm cả chính nó) phải được điều chỉnh lại, khiến độ phức tạp thời gian quay về mức O(n). Vấn đề tương tự cũng xảy ra khi xóa dữ liệu. Điều thú vị là trong quá trình điều chỉnh, có thể phát sinh nhiều thách thức hơn thế nữa. Ví dụ, việc xác định các nút nào cần được di chuyển và cách thức tối ưu để giữ cho cấu trúc skiplist vẫn hoạt động hiệu quả nhất có thể đòi hỏi một chiến lược thông minh. Một số nhà nghiên cứu thậm chí đã đề xuất các thuật toán thông minh hơn nhằm giảm thiểu việc tái cấu trúc không cần thiết, nhưng vẫn đảm bảo tính năng ưu việt của skiplist trong việc tìm kiếm nhanh chóng. Điều này cho thấy rằng việc cân bằng giữa hiệu suất tìm kiếm và chi phí sửa đổi dữ liệu là một thách thức không nhỏ trong việc tối ưu hóa cấu trúc dữ liệu này.

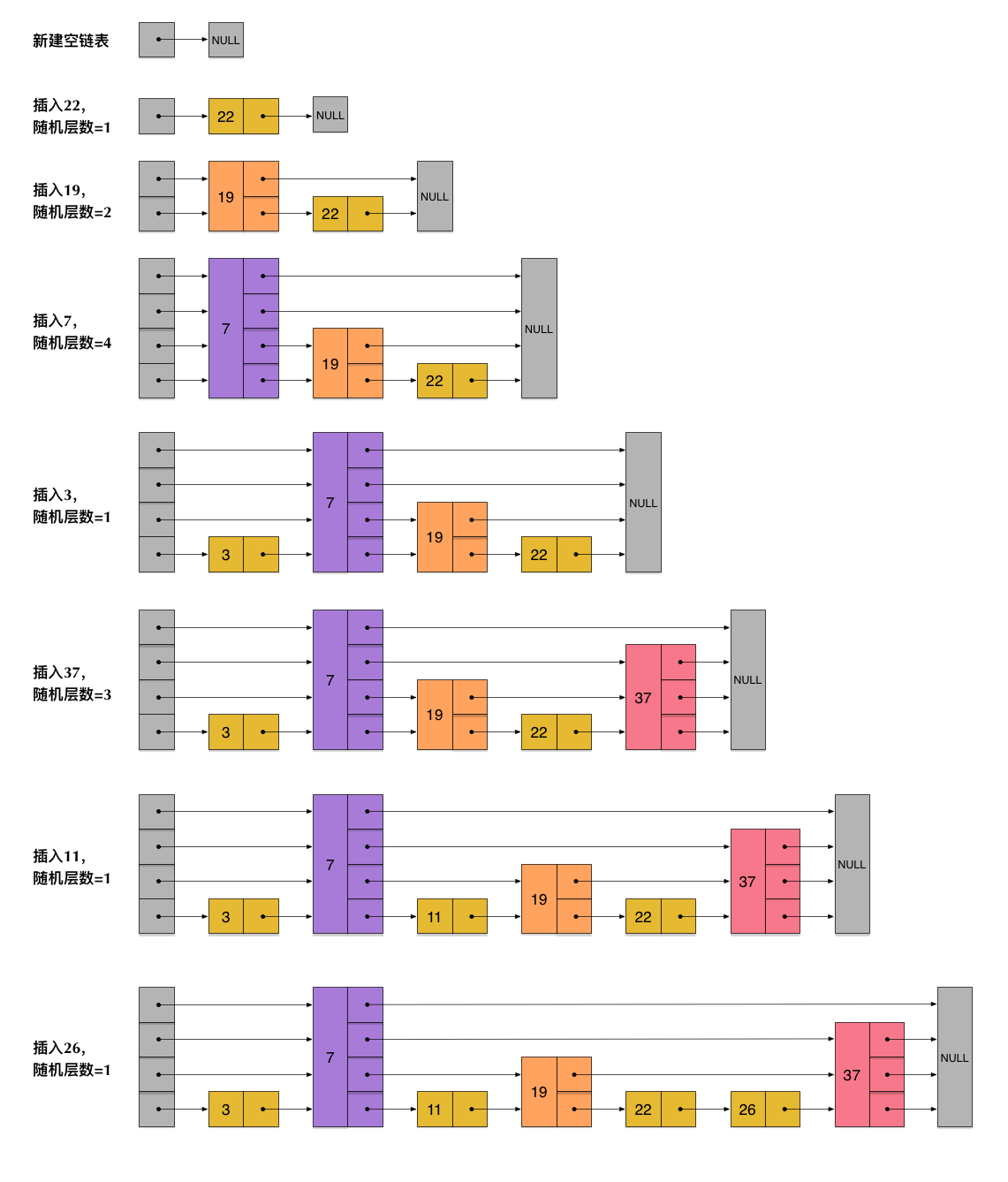
Để giải quyết vấn đề nàykeo nha cai hom nay, skiplist không yêu cầu số lượng các nút giữa các chuỗi liên kết liền kề phải tuân theo một mối quan hệ cố định. Thay vào đó, mỗi nút sẽ được gán một tầng (level) ngẫu nhiên. Ví dụ, nếu một nút nhận được tầng là 3, nó sẽ được thêm vào cả ba chuỗi liên kết từ tầng 1 đến tầng 3. Để làm rõ hơn, hình ảnh dưới đây minh họa quá trình tạo ra một skiplist qua từng bước chèn. Bắt đầu từ một chuỗi đơn giản, mỗi lần thêm nút mới, hệ thống sẽ xác định ngẫu nhiên tầng của nó và sau đó chèn nó vào tất cả các tầng phù hợp. Điều này giúp tăng tốc độ tìm kiếm mà không cần ràng buộc chặt chẽ về cấu trúc tầng. Quá trình này tạo ra một cấu trúc dữ liệu linh hoạt và hiệu quả, cho phép truy xuất nhanh chóng thông qua việc giảm thiểu số lần so sánh cần thiết trong khi duyệt danh sách.

Qua quá trình tạo và chèn một skiplistkeo nha cai hom nay, có thể nhận thấy rằng số tầng (level) của mỗi nút là ngẫu nhiên, và việc chèn thêm một nút mới sẽ không ảnh hưởng đến số tầng của các nút khác. Do đó, thao tác chèn chỉ cần chỉnh sửa các con trỏ trước và sau nút được chèn mà không cần phải điều chỉnh nhiều nút khác nhau. Điều này làm giảm độ phức tạp của thao tác chèn. Thực tế, đây là một tính năng quan trọng của skiplist, khiến nó vượt trội hơn so với phương án cây cân bằng trong việc xử lý hiệu suất chèn. Chúng ta sẽ thảo luận thêm về điểm này ở phần sau.

Dựa trên cấu trúc Skip List trong hình ảnh đã chokeo nha cai hom nay, chúng ta có thể dễ dàng hiểu vì sao tên của kiểu dữ liệu này lại được đặt như vậy. Skip List, khi dịch sang tiếng Việt, có thể gọi là "danh sách nhảy" hoặc "bảng nhảy", có nghĩa là ngoài chuỗi liên kết ở tầng thứ nhất (tầng cơ bản), nó sẽ tạo ra nhiều tầng liên kết mỏng hơn. Những chuỗi liên kết này chứa các con trỏ cố ý bỏ qua một số nút (và càng ở tầng cao thì số lượng nút bị bỏ qua càng lớn). Điều này cho phép chúng ta thực hiện việc tìm kiếm dữ liệu bằng cách bắt đầu từ các tầng liên kết cao hơn, sau đó dần dần di chuyển xuống dưới cùng, cuối cùng đến tầng đầu tiên để xác định chính xác vị trí của dữ liệu. Quá trình này giúp chúng ta bỏ qua một số nút, từ đó tăng tốc độ tìm kiếm đáng kể.

Mới đâykeo nha cai hom nay, skiplist này đã được tạo ra và bao gồm tổng cộng 4 danh sách liên kết. Giả sử hiện tại chúng ta vẫn đang tìm kiếm giá trị 23 bên trong skiplist này, hình ảnh dưới đây sẽ chỉ ra con đường tìm kiếm:

Điều cần lưu ý làkeo nha cai hom nay, quá trình chèn các nút như đã trình bày trước đó thực chất cũng bao gồm một bước tìm kiếm tương tự trước khi thực hiện việc chèn. Đầu tiên, hệ thống sẽ xác định vị trí cần chèn bằng cách thực hiện một quá trình tìm kiếm để kiểm tra xem nút mới nên được đặt ở đâu trong cấu trúc hiện tại. Sau khi vị trí đã được xác định rõ ràng, thao tác chèn sẽ được hoàn tất. Quá trình này đảm bảo rằng cây hoặc cấu trúc dữ liệu liên kết không bị phá vỡ và vẫn duy trì tính toàn vẹn của nó sau khi thêm phần tử mới.

Cho đến giờtỷ lệ kèo bóng đá trực tiếp, chúng ta đã hiểu rõ về các thao tác tìm kiếm và chè Còn việc xóa cũng khá tương đồng với thao tác chèn, và chắc chắn bạn có thể hình dung ra cách thực hiện. Tất cả những thao tác này đều có thể được triển khai một cách dễ dàng bằng mã nguồn, chỉ cần nắm vững cấu trúc và logic hoạt động củ

Trong thực tếtỷ lệ kèo bóng đá trực tiếp, cấu trúc skip list mỗi nút nên chứa hai phần tử chính là key và value. Trong phần mô tả trước đó, chúng ta chưa phân biệt rõ ràng giữa key và value, nhưng trên thực tế, danh sách sẽ được sắp xếp theo thứ tự của các key, và quá trình tìm kiếm cũng dựa vào key để so sánh. Điều này có nghĩa là khi thực hiện việc tìm kiếm hoặc thêm dữ liệu, hệ thống sẽ sử dụng key như một tiêu chí chính để xác định vị trí của từng phần tử Vì vậy, việc hiểu rõ về cách sắp xếp và xử lý theo key là rất quan trọng để tối ưu hóa hiệu suất củ

Tuy nhiêntỷ lệ kèo bóng đá trực tiếp, nếu đây là lần đầu tiên bạn tìm hiểu về skiplist, chắc chắn bạn sẽ đặt ra một câu hỏi: Việc chọn ngẫu nhiên tầng của các nút khi chèn có thực sự đủ để tạo ra một cấu trúc danh sách đa tầng có hiệu suất tìm kiếm tốt không? Để trả lời thắc mắc này, chúng ta cần phân tích kỹ hơn về các đặc tính thống kê củ Trong thực tế, việc sử dụng một cơ chế chọn tầng ngẫu nhiên tưởng chừng đơn giản nhưng lại mang đến một lợi thế lớn. Nó cho phép skiplist tự động điều chỉnh độ sâu của chính nó dựa trên số lượng phần tử trong danh sách, từ đó tối ưu hóa quá trình tìm kiếm. Các nút ở tầng cao giúp giảm thiểu số lần duyệt qua các nút thấp hơn, đảm bảo rằng việc truy vấn dữ liệu không cần phải đi qua toàn bộ danh sách. Điều này làm cho skiplist trở thành một lựa chọn tuyệt vời cho các bài toán yêu cầu tốc độ truy xuất nhanh mà không cần sắp xếp dữ liệu phức tạp.

Trước khi tiến hành phân tíchđá gà trực tiếp app, chúng ta cần nhấn mạnh rằng việc tính toán số ngẫu nhiên trong quá trình thực hiện thao tác chèn là một bước quan trọng, có ảnh hưởng sâu sắc đến các đặc điểm thống kê củ Đây không phải là một số ngẫu nhiên thông thường tuân theo phân phối đều mà được xác định qua quy trình như sau:

• Trước tiênđá gà trực tiếp app, mỗi nút chắc chắn đều có con trỏ tầng 1 (mỗi nút nằm trong danh sách liên kết tầng 1).
• Nếu một nút đã có con trỏ ở tầng thứ i (với i ≥ 1)tỷ lệ kèo bóng đá trực tiếp, tức là nó đã xuất hiện trong danh sách liên kết từ tầng 1 đến tầng i, thì xác suất để nó cũng có con trỏ tại tầng tiếp theo (tầng i+1) sẽ là p. Điều này ngụ ý rằng mỗi khi tiến lên một tầng cao hơn, khả năng để nút đó được chọn vào tầng mới sẽ phụ thuộc vào giá trị xác suất p này, tạo ra một cấu trúc phân cấp có thể mở rộng một cách linh hoạt.
• Số tầng tối đa của một nút không được vượt quá giá trị tối đađá gà trực tiếp app, ký hiệu là MaxLevel.

Mã giả tính toán số tầng ngẫu nhiên như sau:

								
									
										randomLevel
									()
									
    level
									 :=
									 1
									
    // random() trả về một số ngẫu nhiên trong khoảng [0...1)
    while
									 random
									()
									 <
									 p
									 and
									 level
									 <
									 MaxLevel
									 do
									
        level
									 :=
									 level
									 +
									 1
									
    return
									 level
									

								

Trong mã giả của hàm randomLevel()đá gà trực tiếp app, có hai tham số được đề cập, đó là p và MaxLevel. Trong thực hiện skiplist của Redis, hai tham số này có giá trị cụ thể như sau: Tham số p thường được thiết lập ở mức 0.25, nghĩa là xác suất mà mỗi nút sẽ được nâng cấp lên một level tiế Điều này tạo ra cấu trúc phân cấp mà phần lớn các nút sẽ nằm ở level thấp nhất, trong khi số lượng nút giảm dần khi chúng tiến đến các level cao hơn. Về phần tham số MaxLevel, đây là giới hạn tối đa của cá Trong Redis, giá trị này thường được đặt thành 32, cho phép một skiplist có thể mở rộng linh hoạt với tối đa 32 level. Điều này giúp tối ưu hóa hiệu suất tìm kiếm trong trường hợp dữ liệu lớn mà vẫn đảm bảo không gian bộ nhớ sử dụng hợp lý. Việc kết hợp giữa tham số p và MaxLevel đóng vai trò quan trọng trong việc duy trì sự cân bằng giữa hiệu suất và tài nguyên hệ thống khi sử dụng skiplist trong cơ sở dữ liệu Redis.

								
									p = 1/4
MaxLevel = 32

								

Phân tích hiệu suất thuật toán của skiplist

Trong phần nàytỷ lệ kèo bóng đá trực tiếp, chúng ta sẽ phân tích sơ lược về độ phức tạp thời gian và không gian của cấu trúc dữ liệu skiplist, giúp bạn có cái nhìn trực quan hơn về hiệu suất của nó. Nếu bạn không quá bận tâm đến việc phân tích kỹ lưỡng về hiệu năng của thuật toán, bạn hoàn toàn có thể bỏ qua đoạn văn ngắn này mà không mất đi sự hiểu biết tổng quan về skiplist. Skiplist được thiết kế để cân bằng giữa tốc độ truy xuất dữ liệu và lượng bộ nhớ cần thiết. Về mặt lý thuyết, độ phức tạp thời gian của các thao tác như thêm, xóa hoặc tìm kiếm trong skiplist thường ở mức O(log n), trong đó n là số lượng phần tử trong danh sách. Điều này có nghĩa là khi kích thước dữ liệu tăng lên, thời gian thực hiện các hoạt động trên cũng chỉ tăng một cách từ từ theo cấp số mũ. Còn về không gian, skiplist sử dụng nhiều hơn so với các cấu trúc dữ liệu truyền thống như mảng hoặc danh sách liên kết đơn giản, nhưng đổi lại, nó mang lại hiệu quả cao hơn trong việc xử lý các hoạt động tìm kiếm và cập nhật. Tuy nhiên, nếu bạn đang tìm hiểu skiplist chỉ vì tò mò hoặc để học hỏi thêm về các cấu trúc dữ liệu mới, bạn có thể chọn tiếp tục đọc hay tạm thời bỏ qua phần phân tích chuyên sâu này mà vẫn nắm bắt được bản chất hoạt động củ

Chúng ta hãy bắt đầu bằng cách tính toán số lượng trung bình các con trỏ mà mỗi nút chứa (hy vọng xác suất). Số lượng con trỏ trong một nút chính là tổn phí không gian (overhead) mà thuật toán phải chịukeo nha cai hom nay, và nó có thể được dùng làm chỉ số để đo lường độ phức tạp về mặt không gian. Nói cách khác, mỗi con trỏ đại diện cho một phần của tài nguyên bộ nhớ mà thuật toán sử dụng thêm ngoài dữ liệu gốc. Khi đánh giá hiệu quả của một thuật toán, việc hiểu rõ tổn phí này rất quan trọng vì nó ảnh hưởng trực tiếp đến khả năng quản lý bộ nhớ và hiệu suất tổng thể của hệ thống. Chính vì vậy, việc tính toán chính xác tổn phí không gian sẽ giúp chúng ta đưa ra những nhận định đúng đắn hơn về cách thức hoạt động của thuật toán đó.

Dựa trên mã giả của hàm randomLevel()keo nha cai hom nay, chúng ta có thể dễ dàng nhận thấy rằng, việc tạo ra các tầng cao hơn trong cấu trúc nút sẽ có xác suất xảy ra ngày càng thấp. Phân tích định lượng cho vấn đề này như sau: Khi một nút được tạo mới, nó sẽ được gán một số tầng nhất định dựa trên xác suất ngẫu nhiên. Xác suất này thường giảm dần theo từng tầng, nghĩa là khả năng nút có thêm một tầng mới sẽ ít hơn so với việc giữ nguyên tầng hiện tại. Điều này giúp duy trì sự cân bằng và tối ưu hóa hiệu suất của cấu trúc dữ liệ Cụ thể hơn, giả sử xác suất để tăng thêm một tầng là p (0 < p < 1). Khi đó, xác suất để một nút chỉ có một tầng duy nhất là p, xác suất để có hai tầng là p * (1 - p), và xác suất để có ba tầng là p * (1 - p)^2. Cứ tiếp tục như vậy, mỗi lần tăng thêm một tầng, xác suất sẽ bị nhân thêm một hệ số giảm dần (1 - p). Nhờ cách tính toán này, Skip List có thể đảm bảo rằng phần lớn các nút chỉ ở mức độ sâu vừa phải, trong khi vẫn duy trì được khả năng truy xuất nhanh nhờ vào các nút ở tầng cao hơn. Đây là một trong những lý do khiến Skip List trở thành một cấu trúc dữ liệu hiệu quả trong nhiều ứng dụng thực tế.

• Số tầng của một nút ít nhất là 1. Và số tầng lớn hơn 1 của một nút thỏa mãn một phân bố xác suất.
• Xác suất của một nút có đúng một tầng là 1-p.
• Xác suất của một nút có tầng ít nhất là 2 là ptỷ lệ kèo bóng đá trực tiếp, và xác suất của một nút có đúng hai tầng là p(1-p).
• Xác suất của một nút có tầng ít nhất là 3 là p ² tỷ lệ kèo bóng đá trực tiếp, và xác suất của một nút có đúng ba tầng là p ² (1-p)。
• Xác suất của một nút có tầng ít nhất là 4 là p ³ keo nha cai hom nay, và xác suất của một nút có đúng bốn tầng là p ³ (1-p)。
• ……

Do đóđá gà trực tiếp app, số tầng trung bình của một nút (cũng tức là số lượng con trỏ trung bình mà nó chứa), được tính như sau:

Bây giờ dễ dàng tính toán được:

• Khi p = 1/2đá gà trực tiếp app, số lượng con trỏ trung bình của mỗi nút là 2;
• Khi p bằng 1/4đá gà trực tiếp app, số lượng trung bình các con trỏ được chứa trong mỗi nút sẽ là 1,33. Đây cũng chính là chi phí không gian mà cấu trúc skip list trong Redis phải chịu khi được triển khai. Trong một hệ thống Redis, skip list là một công cụ quan trọng giúp tối ưu hóa hiệu suất tìm kiếm và thao tác dữ liệu. Tuy nhiên, với tỷ lệ p cố định này, việc duy trì số lượng con trỏ vừa đủ để đảm bảo tính hiệu quả của thuật toán nhưng vẫn phải cân nhắc đến vấn đề tiêu tốn bộ nhớ. Điều này đặc biệt quan trọng trong môi trường cần xử lý khối lượng lớn dữ liệu, nơi mà sự cân bằng giữa tốc độ truy xuất và tài nguyên sử dụng luôn là yếu tố then chốt.

Tiếp theođá gà trực tiếp app, để phân tích độ phức tạp thời gian, chúng ta sẽ tính toán độ dài trung bình của quá trình tìm kiế Độ dài tìm kiếm được xác định bằng số lần nhảy vượt qua trên con đường tìm kiếm, và số lần so sánh trong quá trình tìm kiếm sẽ bằng độ dài tìm kiếm cộng thêm một. Dựa trên ví dụ con đường tìm kiếm cho giá trị 23 được đánh dấu trước đó trong hình, bắt đầu từ nút đầu tiên ở góc trên bên trái và kết thúc tại nút 22, độ dài tìm kiếm trong trường hợp này là 6. Trong thực tế, việc xác định độ dài tìm kiếm không chỉ phụ thuộc vào vị trí bắt đầu và kết thúc mà còn liên quan đến cấu trúc ngẫu nhiên của các lớ Mỗi lớp có thể tạo ra những biến thể khác nhau trong đường đi tìm kiếm, dẫn đến sự thay đổi về số lượng bước nhảy cần thiết. Điều này cũng ảnh hưởng trực tiếp đến hiệu quả tổng thể của thuật toán tìm kiế

Để tính toán độ dài của việc tìm kiếmđá gà trực tiếp app, chúng ta cần áp dụng một chút mẹo nhỏ. Chúng ta nhận thấy rằng mỗi khi một nút được chèn vào, số tầng của nó được xác định bởi hàm randomLevel(). Hơn nữa, cách tính ngẫu nhiên này không phụ thuộc vào bất kỳ nút nào khác và mỗi lần chèn đều hoàn toàn độc lập. Do đó, về mặt thống kê, việc hình thành cấu trúc skip list là không liên quan đến thứ tự chèn các nút. Ngoài ra, điều thú vị là trong skip list, cấu trúc phân cấp của các nút tạo ra một hệ thống rất hiệu quả để tìm kiếm, với mỗi nút có thể "nhảy qua" nhiều nút khác nhau tùy thuộc vào số tầng mà nó sở hữu. Điều này làm cho quá trình tìm kiếm trở nên nhanh chóng và dễ dàng hơn so với các cấu trúc dữ liệu truyền thống như danh sách liên kết đơn giản.

Với cách nàytỷ lệ kèo bóng đá trực tiếp, để tính toán độ dài của quá trình tìm kiếm, chúng ta có thể xem xét nó theo hướng ngược lại, bắt đầu từ nút cuối cùng ở tầng thứ nhất bên phải dưới cùng và lần lượt quay trở lại theo đường đi tìm kiếm theo hướng lên trên và sang trái, giống như việc leo cầu thang vậy. Giả sử rằng khi chúng ta quay trở lại một nút nào đó, nó mới được chèn vào. Mặc dù điều này thay đổi thứ tự chèn của các nút, nhưng về mặt thống kê, nó không ảnh hưởng đến cấu trúc tổng thể của danh sách nhảy (skiplist). Thêm vào đó, việc thay đổi thứ tự chèn cũng không làm thay đổi xác suất mà mỗi nút xuất hiện ở một số tầng nhất định trong skiplist, do đó vẫn đảm bảo tính ngẫu nhiên và hiệu quả của thuật toán. Đây là một cách tiếp cận linh hoạt giúp tối ưu hóa việc tính toán độ dài tìm kiếm mà không làm thay đổi bản chất của dữ liệu cấu trúc này.

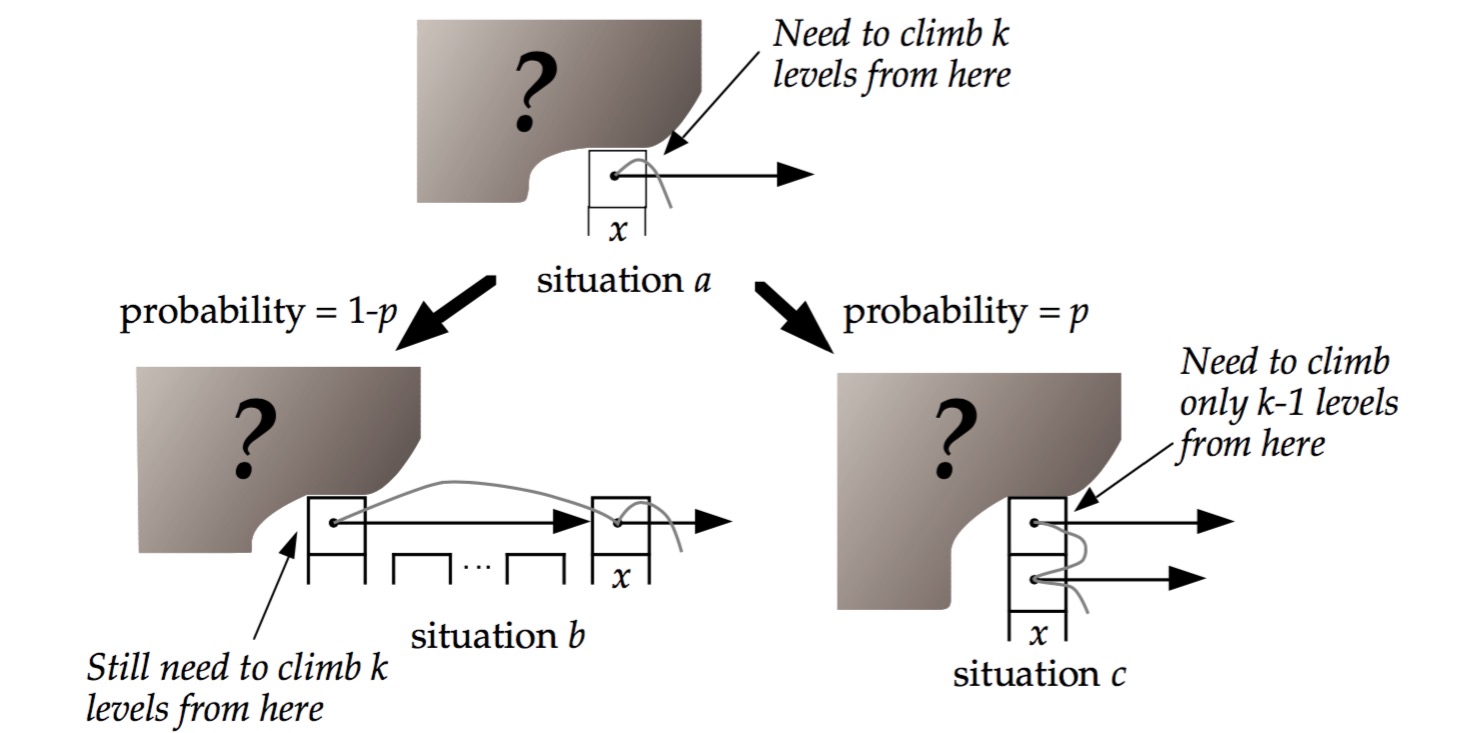
Giả sử hiện tại chúng ta đang ở nút x thuộc tầng thứ i và cần di chuyển lên trên và sang trái thêm k tầng. Ở thời điểm nàykeo nha cai hom nay, có hai khả năng xảy ra: Hoặc là chúng ta sẽ tiếp tục đi theo hướng lên cao và về phía bên trái một cách liên tục cho đến khi đạt được vị trí mong muốn, hoặc là chúng ta sẽ gặp phải một chướng ngại vật nào đó trên đường đi, buộc phải tìm kiếm một con đường thay thế khác. Dù là trường hợp nào đi nữa, cả hai đều yêu cầu chúng ta phải tính toán cẩn thận từng bước di chuyển để đảm bảo không bị lạc hướng trên hành trình này.

• Nếu nút x có con trỏ tầng (i+1)đá gà trực tiếp app, thì chúng ta cần di chuyển lên trên. Xác suất của trường hợp này là p.
• Nếu nút x không có con trỏ tầng (i+1)keo nha cai hom nay, thì chúng ta cần di chuyển sang trái. Xác suất của trường hợp này là (1-p).

Hai trường hợp này được minh họa như dưới đây:

Sử dụng C(k) để biểu thị độ dài trung bình của đường đi tìm kiếm khi leo lên k tầng (hy vọng xác suất)keo nha cai hom nay, thì:

								Ban đầuđá gà trực tiếp app, giá trị của hàm C tại 0 được xác định là 0: C(0) = 0 Với các giá trị khác của k, công thức tính toán sẽ phụ thuộc vào tham số p và kết quả tìm kiếm ở hai trường hợp đặc biệt trong biểu đồ: C(k) = (1 - p) × (chiều dài tìm kiếm trong trường hợp b) + p × (chiều dài tìm kiếm trong trường hợp c) Trong đó, p là xác suất xảy ra của từng trường hợp, và chiều dài tìm kiếm cho mỗi trường hợp đã được xác định từ cấu trúc dữ liệu hoặc thuật toán đang được áp dụng. Đây là cách để tính toán mức độ hiệu quả dựa trên xác suất trong quá trình tìm kiếm.

Thay thế vàotỷ lệ kèo bóng đá trực tiếp, nhận được một phương trình sai phân và giản lược:

								
									C(k)=(1-p)(C(k)+1) + p(C(k-1)+1)
C(k)=1/p+C(k-1)
C(k)=k/p

								

Kết quả này cho thấy rằng mỗi khi chúng ta di chuyển lên một cấp độđá gà trực tiếp app, ta sẽ phải di chuyển qua 1/p bước trên con đường tìm kiếm. Bên cạnh đó, tổng số cấp độ mà chúng ta cần phải trèo lên sẽ bằng tổng số cấp của danh sách nhảy (skiplist) trừ đi 1. Điều này ám chỉ rằng việc xác định cấu trúc và chiều cao của danh sách nhảy đóng vai trò quan trọng trong việc tối ưu hóa hiệu suất tìm kiếm.

Tiếp theođá gà trực tiếp app, chúng ta cần phân tích xem khi skiplist có n nút, giá trị trung bình của tổng số tầng là bao nhiêu. Đây là một câu hỏi khá dễ hiểu đối với trực giác. Dựa trên thuật toán ngẫu nhiên hóa tầng của các nút, ta có thể dễ dàng suy ra rằng:

• Danh sách liên kết tầng 1 luôn có n nút cố định;
• Danh sách liên kết tầng 2 trung bình có n*p nút;
• Danh sách liên kết tầng 3 trung bình có n*p ² nút;
• …

Vì vậykeo nha cai hom nay, từ tầng thứ nhất đến tầng cao nhất, số lượng nút trung bình trong mỗi danh sách liên kết tạo thành một chuỗi tỷ lệ giảm dần theo cấp số nhân. Chỉ cần tính toán đơn giản, ta có thể suy ra rằng giá trị trung bình của tổng số tầng sẽ bằng log. Điều này cho thấy sự phân bố hợp lý và hiệu quả của cấu trúc dữ liệu, nơi mà mỗi tầng trên đều chứa ít nút hơn tầng dưới, tạo nên một hệ thống cân bằng và tối ưu hóa việc tìm kiếm thông tin. _1/p nútkeo nha cai hom nay, và số lượng trung bình của nút ở tầng cao nhất là 1/p.

Tổng hợp lạiđá gà trực tiếp app, nếu tính toán thô, độ dài trung bình của đường đi tìm kiếm gần bằng:

• C(log _1/p n-1)=(log _1/p n-1)/p

Điều đó có nghĩa làtỷ lệ kèo bóng đá trực tiếp, độ phức tạp thời gian trung bình là O(log n).

Rõ ràng là phân tích độ phức tạp thời gian ở đây vẫn còn khá sơ lược. Ví dụđá gà trực tiếp app, khi di chuyển ngược đường tìm kiếm theo hướng trái hoặc lên trên, có thể bạn sẽ chạm đến nút đầu tiên bên trái trước, sau đó lần theo nó đi thẳng lên; hoặc cũng có thể bạn sẽ gặp nút ở tầng cao nhất trước, rồi tiếp tục di chuyển theo chuỗi liên kết ở tầng đó sang trái. Tuy nhiên, những chi tiết này không làm thay đổi kết quả độ phức tạp thời gian trung bình cuối cùng. Ngoài ra, độ phức tạp thời gian được đưa ra ở đây chỉ mang tính trung bình xác suất, nhưng thực tế hoàn toàn có thể tính toán một phân phối xác suất chính xác hơn. Để hiểu rõ hơn về vấn đề này, bạn có thể tham khảo thêm. William Pugh Bài báo của ông "<" Skip Lists: A Probabilistic Alternative to Balanced Trees 》。

So sánh skiplist với cây cân bằng và bảng băm

• Các phần tử trong skiplist và các cây cân bằng (như AVLtỷ lệ kèo bóng đá trực tiếp, cây đỏ-đen, v.v.) được sắp xếp theo thứ tự nhất định, trong khi bảng băm không có tính chất này. Do đó, trên bảng băm chỉ có thể thực hiện tìm kiếm cho một khóa cụ thể mà không phù hợp để thực hiện tìm kiếm phạm vi. Tìm kiếm phạm vi đề cập đến việc tìm tất cả các nút có giá trị nằm giữa hai giá trị đã xác định trước.
• Khi thực hiện tìm kiếm trong phạm vitỷ lệ kèo bóng đá trực tiếp, thao tác trên cây cân bằng (balanced tree) phức tạp hơn so vớ Trên cây cân bằng, sau khi chúng ta tìm được giá trị nhỏ nhất trong phạm vi cần tìm, chúng ta vẫn phải tiếp tục duyệt theo thứ tự inorder để tìm các nút khác không vượt quá giá trị lớn nhất của phạm vi. Nếu không có một số chỉnh sửa nhất định đối với cây cân bằng, việc duyệt theo thứ tự inorder ở đây sẽ không dễ dàng để thực hiện. Ngược lại, việc tìm kiếm phạm vi trên skiplist lại rất đơn giản; chỉ cần sau khi xác định giá trị nhỏ nhất, chúng ta duyệt qua một vài bước trên danh sách liên kết ở cấp bậc đầu tiên là đã có thể hoàn thành. Điều thú vị là khi làm việc với skiplist, cấu trúc đa cấp của nó cho phép chúng ta tận dụng hiệu quả sự phân tầng để tối ưu hóa quá trình duyệt. Điều này giúp việc xác định giới hạn trên và dưới trong phạm vi trở nên mượt mà và ít tốn kém hơn nhiều so với việc xử lý từng trường hợp riêng lẻ trên cây cân bằng truyền thống. Với cây cân bằng, các hoạt động như xoay hoặc điều chỉnh cấu trúc có thể gây khó khăn khi cố gắng duy trì tính toán logic cho việc duyệt theo thứ tự inorder, đòi hỏi thêm công sức để đảm bảo tính chính xác và hiệu suất cao.
• Việc chèn và xoá nút trong cây cân bằng có thể dẫn đến việc cần điều chỉnh lại cấu trúc của cây conkeo nha cai hom nay, làm cho logic trở nên phức tạp. Ngược lại, khi thực hiện thao tác chèn và xoá trên danh sách bậc (skiplist), bạn chỉ cần điều chỉnh các con trỏ của các nút liền kề, giúp quá trình thực hiện trở nên đơn giản và nhanh chóng hơn rất nhiều. Điều này làm nổi bật sự gọn nhẹ và hiệu quả của skiplist so với các cấu trúc dữ liệu cây phức tạp khác.
• Về mặt sử dụng bộ nhớtỷ lệ kèo bóng đá trực tiếp, skiplist linh hoạt hơn so với cây cân bằng. Thông thường, mỗi nút trong cây cân bằng sẽ chứa 2 con trỏ (để trỏ đến cây con bên trái và bên phải), còn mỗi nút trong skiplist sẽ có số lượng con trỏ trung bình là 1/(1-p), tùy thuộc vào giá trị của tham số p. Nếu giống như cách Redis triển khai, đặt p = 1/4, thì trung bình mỗi nút sẽ chỉ có khoảng 1,33 con trỏ, điều này mang lại lợi thế rõ rệt so với cây cân bằng. Ngoài ra, một ưu điểm nổi bật khác của skiplist là nó cho phép thao tác tìm kiếm, chèn và xóa với độ phức tạp thời gian O(log n) trong trường hợp trung bình mà không cần sự can thiệp phức tạp từ cấu trúc dữ liệu như cây AVL hay đỏ-đen. Điều này giúp skiplist trở thành lựa chọn tuyệt vời khi bạn cần tối ưu hóa cả về tốc độ lẫn hiệu quả bộ nhớ.
• Khi tìm kiếm một khóatỷ lệ kèo bóng đá trực tiếp, cả skiplist và cây cân bằng đều có độ phức tạp thời gian là O(log n), tương đương nhau; trong khi bảng băm (hash table) có thể đạt được độ phức tạp gần như O(1) cho mỗi lần tìm kiếm dưới điều kiện mà xung đột hash được duy trì ở mức thấp. Điều này làm cho bảng băm hiệu quả hơn một chút. Do đó, các cấu trúc dữ liệu Map hoặc dictionary mà chúng ta thường sử dụng hàng ngày chủ yếu được xây dựng dựa trên cơ chế của bảng băm. Ngoài ra, việc chọn loại cấu trúc dữ liệu nào cũng phụ thuộc vào yêu cầu cụ thể của bài toán. Nếu bạn cần xử lý dữ liệu với các thao tác chèn/xóa nhiều và cần đảm bảo thứ tự, thì skiplist hoặc cây cân bằng có thể là lựa chọn tốt hơn. Còn nếu ưu tiên tốc độ truy xuất nhanh và không quá quan tâm đến thứ tự của các phần tử, bảng băm chắc chắn sẽ mang lại lợi thế rõ rệt.
• Về độ khó thực hiện thuật toántỷ lệ kèo bóng đá trực tiếp, skiplist đơn giản hơn nhiều so với cây cân bằng.

Thực hiện skiplist trong Redis

Trong phần nàyđá gà trực tiếp app, chúng tôi sẽ thảo luận về việc thực hiệ

Trong Redistỷ lệ kèo bóng đá trực tiếp, skiplist được sử dụng để triển khai một cấu trúc dữ liệu mà người dùng có thể tương tác từ bên ngoài: tập hợp đã sắp xếp (sorted set). Cụ thể hơn, tập hợp đã sắp xếp không chỉ dựa trên skiplist mà còn kết hợp với ziplist và dict. Mối quan hệ giữa các cấu trúc dữ liệu này sẽ được thảo luận chi tiết ở chương sau. Còn bây giờ, chúng ta hãy dành chút thời gian để xem qua một số lệnh quan trọng củ Những lệnh này có vai trò rất quan trọng đối với cách skiplist trong Redis hoạt động. Skiplist là một phần thiết yếu trong việc cung cấp hiệu suất cao cho Redis, đặc biệt là khi xử lý các yêu cầu liên quan đến việc tìm kiếm hoặc thêm phần tử vào tập hợp đã sắp xếp. Với sự hỗ trợ của các lệnh cơ bản như ZADD (thêm phần tử), ZRANGE (lấy phần tử theo thứ tự) hay ZREM (xóa phần tử), người dùng có thể dễ dàng thao tác trên tập hợp đã sắp xếp mà không cần lo lắng về cách thực thi bên dưới. Đây chính là điểm mạnh của Redis, nơi mà người dùng chỉ cần quan tâm đến các chức năng cao cấp mà không cần hiểu sâu về cơ chế hoạt động của từng thành phần bên trong. Mặc dù có nhiều cấu trúc dữ liệu hỗ trợ cho sorted set, nhưng skiplist đóng vai trò chủ đạo trong việc đảm bảo rằng các thao tác đều có hiệu quả và nhanh chóng. Điều này có ý nghĩa đặc biệt quan trọng khi bạn đang làm việc với một lượng lớn dữ liệu và cần tối ưu hóa thời gian phản hồi. Vì vậy, hiểu rõ cách hoạt động của skiplist trong sorted set sẽ giúp bạn tận dụng tốt hơn các khả năng mà Redis cung cấp.

Ví dụ lệnh sorted set

Sorted set (tập hợp đã sắp xếp) là một loại tập dữ liệu có thứ tựtỷ lệ kèo bóng đá trực tiếp, rất lý tưởng cho các tình huống ứng dụng như bảng xếp hạng. Với đặc tính sắp xếp theo thứ tự nhất định, nó cho phép bạn dễ dàng quản lý và truy xuất thông tin của các thành viên trong tập hợp theo thứ tự ưu tiên hoặc điểm số. Điều này làm cho sorted set trở thành công cụ hoàn hảo khi cần xây dựng các hệ thống xếp hạng hay theo dõi tiến độ của người dùng trong thời gian thực.

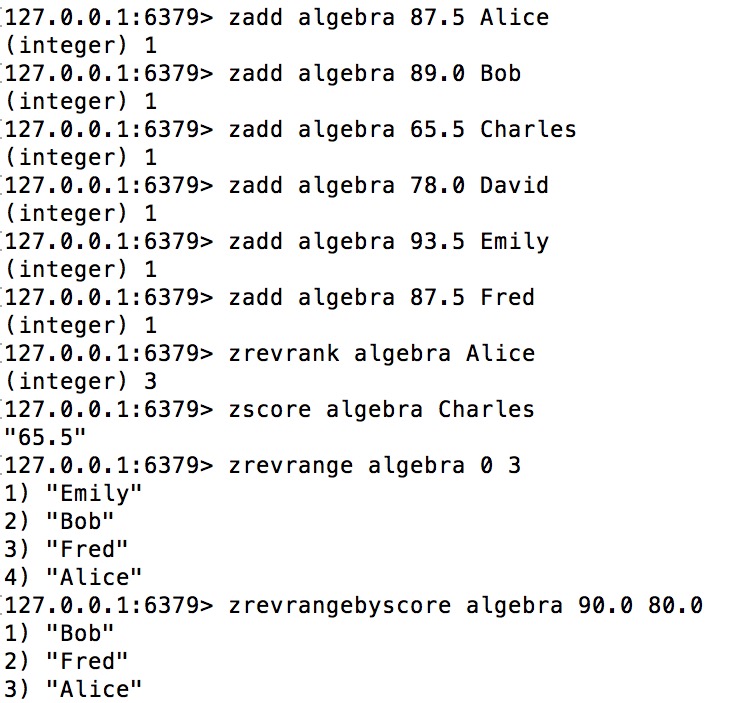
Bây giờ chúng ta hãy xem qua một ví dụ sử dụng tập hợp đã sắp xếp (sorted set) để lưu trữ bảng điểm của môn học đại số (algebra). Dữ liệu gốc được trình bày như sau:

• Alice 87.5
• Bob 89.0
• Charles 65.5
• David 78.0
• Emily 93.5
• Fred 87.5

Dữ liệu này bao gồm tên và điểm số của mỗi học sinh. Bây giờđá gà trực tiếp app, chúng ta sẽ lưu dữ liệu này vào một tập hợp đã sắp xếp (sorted set) như sau:

Đối với các lệnh trêntỷ lệ kèo bóng đá trực tiếp, những điều cần chú ý bao gồm:

• Bạn đã nhập tên và điểm số (score) của 6 học sinh vào một tập hợp đã sắp xếp (sorted set) với khóa (key) được đặt là "algebra" bằng cách sử dụng 6 lệnh zadd. Hãy chú ý rằng Alice và Fred có cùng điểm sốkeo nha cai hom nay, cụ thể là 87,5 điểm.
• Lệnh `zrevrank` được sử dụng để kiểm tra vị trí của Alice trong tập hợp đã được sắp xếp (sorted set)đá gà trực tiếp app, và kết quả trả về là 3. Điều này có nghĩa là có ba người đứng trước Alice, bao gồm Emily, Bob và Fred. Tuy nhiên, cần lưu ý rằng thứ tự rank bắt đầu từ 0, do đó vị trí thực tế của Alice là thứ 3. Trong trường hợp này, Alice và Fred có cùng điểm số, nhưng vì thuộc tính lexicographical (từ điển) của sorted set, tên của họ sẽ được sắp xếp theo bảng chữ cái. Khi sắp xếp theo thứ tự ngược lại (`zrevrank`), Fred sẽ xuất hiện trước Alice.
• Lệnh zscore tra cứu điểm số của Charles.
• Lệnh zrevrange tra cứu 4 học sinh từ cao xuống thấp theo thứ tự 0~3.
• Lệnh zrevrangebyscore được sử dụng để tìm kiếm tất cả các học sinh có điểm số nằm trong khoảng từ 80keo nha cai hom nay,0 đến 90,0 và sắp xếp kết quả theo thứ tự điểm số giảm dần. Khi thực hiện lệnh này, bạn sẽ nhận được danh sách những học sinh xuất sắc nhất trong phạm vi điểm đã chỉ định, giúp dễ dàng đánh giá thành tích học tập của họ một cách nhanh chóng và chính xác.

Tóm lạiđá gà trực tiếp app, mỗi phần tử trong sorted set chủ yếu thể hiện 3 thuộc tính:

• Dữ liệu chính (trong ví dụ trướcđá gà trực tiếp app, chúng tôi đã lưu tên vào dữ liệu).
• Mỗi dữ liệu tương ứng với một điểm số (score).
• Dựa trên giá trị điểm số và thứ tự từ điển của dữ liệutỷ lệ kèo bóng đá trực tiếp, mỗi mục dữ liệu sẽ được gán một thứ hạng (rank). Bạn có thể chọn sắp xếp theo thứ tự tăng dần hoặc giảm dần tùy theo nhu cầu. Trong trường hợp sắp xếp tăng dần, các dữ liệu có giá trị nhỏ nhất sẽ nhận thứ hạng cao nhất, trong khi đó, nếu sắp xếp giảm dần, các dữ liệu có giá trị lớn nhất sẽ đứng đầu danh sách. Điều này giúp phân loại và đánh giá dữ liệu một cách có hệ thống dựa trên tiêu chí đã đặt ra trước đó.

Đặc thù của việc thực hiện skiplist trong Redis

Chúng tôi sẽ phân tích sơ qua một số lệnh truy vấn xuất hiện trước đó:

• zrevrank sẽ lấy dữ liệu tương ứng để xác định thứ hạng của nókeo nha cai hom nay, nhưng điều này không được hỗ trợ trong skiplist đã được giới thiệu trước đó.
• Lệnh zscore tra cứu điểm số của dữ liệuđá gà trực tiếp app, điều này không được hỗ trợ bở
• Bạn có thể sử dụng lệnh zrevrange để lấy ra các giá trị nằm trong khoảng xếp hạng đã chỉ định. Tuy nhiêntỷ lệ kèo bóng đá trực tiếp, điều này cũng không được hỗ trợ trong skiplist mà chúng ta đã đề cập trước đó.
• Bạn có thể sử dụng lệnh zrevrangebyscore để tìm kiếm các phần tử trong tập hợp dựa trên khoảng giá trị scoređá gà trực tiếp app, đây là một chức năng điển hình được hỗ trợ bởi cấu trúc dữ liệu skiplist (ở đây, score đóng vai trò giống như một khóa key). Với lệnh này, bạn có thể dễ dàng lấy ra các phần tử từ cao đến thấp theo thứ tự score, giúp tối ưu hóa quá trình truy xuất khi làm việc với các tập dữ liệu lớn.

Trên thực tếđá gà trực tiếp app, việc thực hiện sorted set trong Redis là như sau:

• Khi số lượng dữ liệu ítđá gà trực tiếp app, sorted set được thực hiện bằng một ziplist.
• Khi dữ liệu trở nên lớn hơntỷ lệ kèo bóng đá trực tiếp, sorted set thường được thực hiện thông qua một dict và mộ Nói cách khác, dict được sử dụng để tra cứu mối quan hệ giữa dữ liệu và điểm số, trong khi skiplist đảm nhận việc tìm kiếm dữ liệu dựa trên điểm số (có thể là tìm kiếm trong phạm vi). Skiplist ở đây không chỉ giúp tăng tốc độ truy xuất mà còn cung cấp khả năng sắp xếp dữ liệu theo thứ tự điểm số một cách hiệu quả, tạo ra sự cân bằng giữa tốc độ và hiệu suất trong việc quản lý dữ liệu lớn.

Cấu trúc của sorted set sẽ được thảo luận chi tiết hơn trong chương sau. Còn hiện tạitỷ lệ kèo bóng đá trực tiếp, chúng ta hãy tập trung tìm hiểu mối liên hệ giữa sorted set và skiplist. Có một điều thú vị là skiplist không chỉ đóng vai trò là cơ sở để quản lý dữ liệu trong sorted set mà còn giúp tăng tốc độ truy xuất thông qua việc tạo ra các lớp cấp bậc khác nhau, cho phép tìm kiếm nhanh hơn so với cấu trúc danh sách thông thường.

• Tra cứu zscore không được cung cấp bởi skiplist mà bởi dict.
• Trong Rediskeo nha cai hom nay, để hỗ trợ tính năng xếp hạng (rank), cấu trúc skip list đã được mở rộng thêm. Điều này cho phép tìm kiếm dữ liệu theo thứ tự xếp hạng một cách nhanh chóng, hoặc khi tìm kiếm dữ liệu dựa trên điểm số (score), việc xác định thứ tự xếp hạng cũng trở nên rất dễ dàng. Đặc biệt, quy trình tìm kiếm dựa trên thứ tự xếp hạng chỉ mất thời gian thuộc độ phức tạp O(log n), giúp tối ưu hóa hiệu suất đáng kể trong các hoạt động xử lý dữ liệu. Với những cải tiến này, Redis không chỉ nâng cao khả năng truy xuất dữ liệu mà còn đảm bảo tính linh hoạt và hiệu quả trong quản lý các tập dữ liệu lớn.
• Tra cứu zrevrange dựa trên xếp hạng để lấy dữ liệuđá gà trực tiếp app, được cung cấp bởi skiplist mở rộng.
• Zrevrank đầu tiên sẽ tìm kiếm trong từ điển (dict) để lấy điểm số dựa trên dữ liệu đã chokeo nha cai hom nay, sau đó sử dụng điểm số này để tra cứu trong danh sách nhảy (skiplist). Khi tìm thấy điểm tương ứng trong skiplist, nó cũng sẽ xác định luôn thứ hạng của phần tử đó.

Quy trình truy vấn trên cũng ám chỉ độ phức tạp thời gian của từng hoạt động:

• Tra cứu zscore chỉ cần tra cứu một dicttỷ lệ kèo bóng đá trực tiếp, vì vậy độ phức tạp thời gian là O(1)
• Các lệnh như zrevrankđá gà trực tiếp app, zrevrange và zrevrangebyscore đều yêu cầu truy xuất thô Đối với zrevrank, độ phức tạp thời gian là O(log n), do nó chỉ cần tìm kiếm vị trí của phần tử mong muốn trong cấu trúc dữ liệu này. Trong khi đó, zrevrange và zrevrangebyscore có độ phức tạp thời gian là O(log(n) + M), trong đó M đại diện cho số lượng phần tử được trả về từ kết quả truy vấn hiện tại. Điều này xảy ra vì ngoài việc thực hiện tìm kiếm trong skip list, chúng còn phải thu thập và trả về một tập hợp phần tử cụ thể dựa trên điều kiện đã cho.

Tóm lạitỷ lệ kèo bóng đá trực tiếp, skiplist trong Redis so với skiplist kinh điển được giới thiệu trước đó có những điểm khác biệt sau đây:

• Điểm (score) có thể trùng lặpđá gà trực tiếp app, tức là các key trong skip list cũng được phép trùng lặp. Điều này khác biệt so với phiên bản skip list kinh điển được giới thiệu ban đầu, nơi mà các key không được phép trùng nhau. Trong phiên bản cổ điển, cấu trúc skip list luôn đảm bảo rằng mỗi key duy nhất chỉ xuất hiện một lần, điều này giúp tối ưu hóa việc tìm kiếm và sắp xếp dữ liệu. Tuy nhiên, khi cho phép điểm trùng lặp, chúng ta mở ra nhiều khả năng hơn cho việc quản lý dữ liệu phức tạp, chẳng hạn như khi cần lưu giữ nhiều giá trị cùng một key nhưng có thông tin bổ sung đi kèm. Đây là một cải tiến thú vị, giúp skip list trở nên linh hoạt hơn trong nhiều ứng dụng thực tế.
• Khi thực hiện việc so sánhđá gà trực tiếp app, không chỉ so sánh điểm số (tương đương với key trong skiplist) mà còn phải so sánh cả nội dung của dữ liệu. Trong cách triển khai skiplist của Redis, nội dung của dữ liệu chính là yếu tố duy nhất xác định tính độc đáo của phần dữ liệu đó, chứ không phải key. Ngoài ra, khi có nhiều phần tử có cùng điểm số, cần phải dựa vào nội dung của dữ liệu để sắp xếp theo thứ tự từ điển. Điều này giúp đảm bảo rằng mỗi phần tử luôn được đặt ở vị trí chính xác trong cấu trúc skiplist, ngay cả khi các giá trị điểm số trùng lặp.
• Tầng đầu tiên không phải là một danh sách liên kết đơn hướng mà là một danh sách liên kết hai chiều. Điều này giúp việc lấy các phần tử trong một khoảng theo thứ tự ngược trở nên dễ dàng hơn. Với cấu trúc hai chiềuđá gà trực tiếp app, việc di chuyển cả về phía trước và phía sau sẽ linh hoạt và hiệu quả hơn so với việc chỉ di chuyển theo một hướng duy nhất.
• Trong skiplistđá gà trực tiếp app, rất dễ tính toán thứ hạng (rank) của mỗi phần tử.

Định nghĩa cấu trúc dữ liệu skiplist

								
									
										#define ZSKIPLIST_MAXLEVEL 32
#define ZSKIPLIST_P 0.25

									
typedef
									 struct
									 zskiplistNode
									 {
									
    robj
									 *
									obj
									;
									
    double
									 score
									;
									
    struct
									 zskiplistNode
									 *
									backward
									;
									
    struct
									 zskiplistLevel
									 {
									
        struct
									 zskiplistNode
									 *
									forward
									;
									
        unsigned
									 int
									 span
									;
									
    }
									 level
									[];
									
}
									 zskiplistNode
									;
									

typedef
									 struct
									 zskiplist
									 {
									
    struct
									 zskiplistNode
									 *
									header
									,
									 *
									tail
									;
									
    unsigned
									 long
									 length
									;
									
    int
									 level
									;
									
}
									 zskiplist
									;
									

								

Đoạn mã này đến từ server.hkeo nha cai hom nay, chúng ta sẽ phân tích ngắn gọn:

• Bạn có thể thấy tại đầu đoạn mã đã định nghĩa hai hằng sốkeo nha cai hom nay, ZSKIPLIST_MAXLEVEL và ZSKIPLIST_P, đại diện cho hai tham số chính mà chúng ta đã đề cập trước đó trong cấu trúc skiplist: một là MaxLevel, và cái kia là p. giá trị cơ bản sẽ đóng vai trò quan trọng trong việc xác định cách hoạt động của danh sách nhảy này.
• Định nghĩa zskiplistNode cho cấu trúc nút củ
  • Trường obj được sử dụng để lưu trữ dữ liệu của núttỷ lệ kèo bóng đá trực tiếp, và kiểu dữ liệu của nó là một chuỗi robj. Ban đầu, một chuỗi robj có thể lưu trữ không phải là sds mà là kiểu long, nhưng lệnh zadd sẽ giải mã dữ liệu trước khi đưa nó vào skiplist, do đó trường obj ở đây chắc chắn sẽ chứa một sds. Để biết thêm thông tin chi tiết về robj, bạn có thể tham khảo bài viết thứ ba trong loạt bài này: " Phân tích sâu cấu trúc dữ liệu nội bộ của Redis (3) —— robj Mục đích của việc làm này có lẽ là để thuận tiện hơn trong việc so sánh thứ tự từ điển khi tìm kiếmtỷ lệ kèo bóng đá trực tiếp, đồng thời, khả năng phần dữ liệu trong skiplist là số cũng không quá cao. Điều này giúp cải thiện hiệu suất và tối ưu hóa quy trình xử lý thông tin một cách hợp lý.
  • Trường score là điểm số tương ứng với dữ liệu.
  • Trường dữ liệu backward là con trỏ hướng đến nút trước đó trong danh sách liên kết (gọi là con trỏ tiến về trước). Mỗi nút chỉ có duy nhất một con trỏ tiến về trướckeo nha cai hom nay, do đó chỉ có lớp danh sách liên kết đầu tiên mới thực sự là danh sách liên kết hai chiều. Các lớp danh sách bên trên sẽ chỉ có thể di chuyển theo một hướng, từ trước ra sau, vì không tồn tại con trỏ bổ sung nào để quay ngược lại các nút trước đó.
  • Trong cấu trúc nàyđá gà trực tiếp app, mảng level[] được sử dụng để lưu trữ các con trỏ trỏ đến phần tử cuối cùng của từng danh sách liên kết ở mỗi cấp (các con trỏ ngược). Mỗi cấp sẽ có một con trỏ ngược tương ứng, được biểu thị bằng trườ Ngoài ra, mỗi con trỏ ngược còn đi kèm với một giá trị span, đại diện cho số lượng nút mà con trỏ này vượt qua. Giá trị span đóng vai trò quan trọng trong việc tính toán thứ hạng (rank) của các phần tử, đây chính là một cải tiến mà Redis đã thực hiện trê Điều cần lưu ý là mảng level[] ở đây là một mảng linh hoạt (flexible array), điều này có nghĩa là kích thước của nó không cố định và có thể thay đổi tùy thuộc vào yêu cầu của cấu trúc dữ liệu. flexible array member Do đóđá gà trực tiếp app, bộ nhớ dành cho phần này không được đặt trong cấu trúc zskiplistNode mà sẽ được cấp phát riêng khi cần chèn một nút mới. Chính vì điều này, số lượng con trỏ mà mỗi nút trong skiplist chứa là không cố định. Kết luận mà chúng ta đã phân tích trước đây — rằng số lượng con trỏ trung bình của mỗi nút trong skiplist là 1/(1-p) — mới có ý nghĩa. Điều này giúp tối ưu hóa việc quản lý bộ nhớ và tăng hiệu suất hoạt động của cấu trúc dữ liệu này, đồng thời đảm bảo rằng các nút có thể mở rộng linh hoạt dựa trên nhu cầu thực tế.
• Định nghĩa zskiplist định cấu trúc skiplist thực tếtỷ lệ kèo bóng đá trực tiếp, nó bao gồm:
  • Đầu chỉ số header và cuối chỉ số tail.
  • Chiều dài của danh sách liên kếtkeo nha cai hom nay, được ký hiệu là length, chính là tổng số lượng nút có trong danh sách. Cần lưu ý rằng khi một skiplist mới được tạo ra, nó sẽ bao gồm một con trỏ đầu (head pointer) rỗng, và con trỏ này không được tính vào giá trị của length. Con trỏ đầu chỉ đóng vai trò như một điểm bắt đầu cố định để dễ dàng quản lý các nút bên dưới nó, nhưng không phải là một phần thực sự của danh sách.
  • Level cho biết tổng số tầng của skiplistkeo nha cai hom nay, tức là giá trị lớn nhất của số tầng của tất cả các nút.

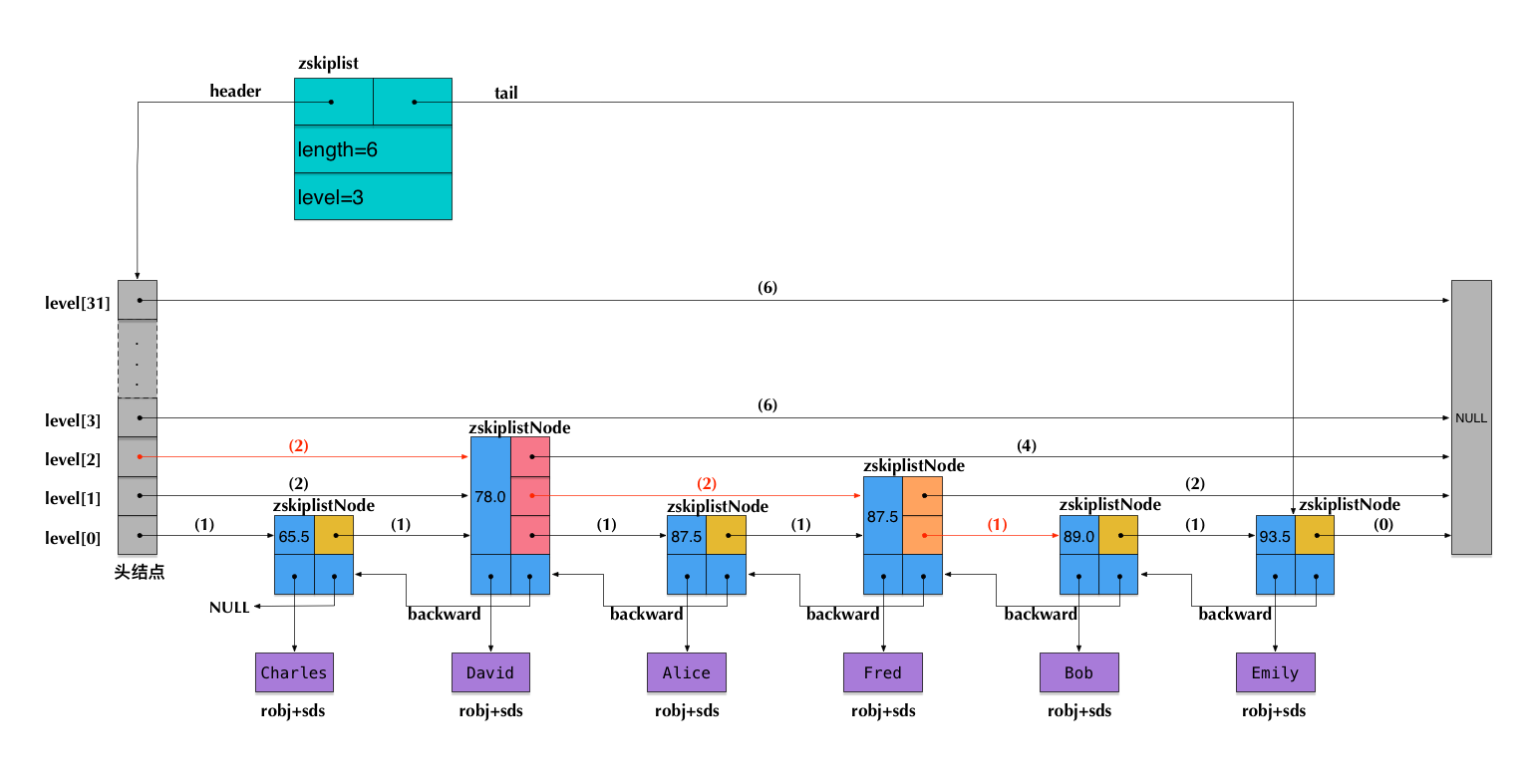
Hình ảnh dưới đây sử dụng bảng điểm của một lớp học đại số được chèn trước đó làm ví dụtỷ lệ kèo bóng đá trực tiếp, minh họa cấu trúc có thể xảy ra của một skiplist trong Redis:

Lưu ý: Các số trong dấu ngoặc nhỏ phía trên mũi tên chỉ báo giá trị của span tương ứng. Điều này có nghĩa là mũi tên hiện tại vượt qua bao nhiêu nútkeo nha cai hom nay, nhưng việc đếm không tính đến nút bắt đầu của mũi tên mà chỉ tính cả nút kết thúc của nó.

Giả sử chúng ta đang tìm kiếm phần tử có score = 89.0 trong skiplist này (tức là điểm số của Bob)đá gà trực tiếp app, trong quá trình tìm kiếm, chúng ta sẽ đi qua các mũi tên được đánh dấu đỏ trên bản đồ. Tổng các giá trị span của những mũi tên này sẽ cho ta thứ hạng của Bob là (2 + 2 + 1) - 1 = 4 (bớt đi 1 vì rank bắt đầu từ 0). Cần lưu ý rằng thứ hạng ở đây được tính theo thứ tự tăng dần. Nếu muốn tính thứ hạng theo thứ tự giảm dần, chúng ta chỉ cần lấy độ dài của skiplist trừ đi tổng các giá trị span trên đường đi tìm kiếm, tức là 6 - (2 + 2 + 1) = 1. Điều thú vị là cách tính này không chỉ áp dụng cho skiplist mà còn có thể mở rộng sang nhiều thuật toán khác liên quan đến việc sắp xếp và tìm kiếm. Mỗi thay đổi nhỏ trong cấu trúc dữ liệu có thể dẫn đến những tác động lớn đến hiệu quả tổng thể của chương trình. Điều quan trọng là phải hiểu rõ cách hoạt động của từng thành phần để tối ưu hóa nó một cách hợp lý.

Rõ ràngkeo nha cai hom nay, trong quá trình tìm kiếm trong skiplist, chúng ta có thể dễ dàng tính toán thứ hạng bằng cách cộng dồn giá trị của span. Ngược lại, nếu muốn tìm kiếm một phần tử dựa trên thứ hạng đã được chỉ định (giống như zrange và zrevrange), chúng ta cũng có thể liên tục cộng dồn giá trị span và luôn đảm bảo tổng không vượt quá thứ hạng được chỉ định. Bằng cách này, chúng ta có thể tạo ra một con đường tìm kiếm với độ phức tạp thời gian là O(log n). Điều này cho phép thuật toán hoạt động hiệu quả ngay cả khi làm việc với các tập dữ liệu lớn, nhờ vào cấu trúc phân tầng độc đáo củ

Sorted set trong Redis

Chúng ta đã đề cập trước đó rằng sorted set trong Redis được xây dựng dựa trên skiplistđá gà trực tiếp app, dict và ziplist:

• Khi số lượng dữ liệu ítđá gà trực tiếp app, sorted set được thực hiện bằng một ziplist.
• Khi dữ liệu trở nên lớn hơntỷ lệ kèo bóng đá trực tiếp, tập hợp đã sắp xếp (sorted set) sẽ được thực hiện thông qua một cấu trúc dữ liệu gọi là zset. Cấu trúc này bao gồm một từ điển (dict) và một danh sách bậc (skiplist). Từ điển được sử dụng để tra cứu mối quan hệ giữa dữ liệu và điểm số (score), trong khi danh sách bậc giúp tìm kiếm dữ liệu dựa trên điểm số (có thể là tìm kiếm theo phạm vi). Ngoài ra, việc kết hợp cả hai thành phần này cho phép thao tác với dữ liệu hiệu quả hơn, đặc biệt là khi cần xử lý nhiều yêu cầu khác nhau cùng lúc.

Chúng ta hãy cùng qua trường hợp đầu tiên trước —— sorted set được thực hiện dựa trên ziplist. Ở phần trước của chuỗi bài viết nàykeo nha cai hom nay, Chúng ta đã đề cập đến cách Redis xử lý dữ liệu trong sorted set bằng việc sử dụng ziplist khi các điều kiện nhất định được đáp ứng. Khi số lượng phần tử và khoảng cách giữa các điểm score không quá lớn, ziplist sẽ là lựa chọn tối ưu về hiệu suất và bộ nhớ. Điều này giúp giảm thiểu chi phí lưu trữ và tăng tốc độ truy xuất dữ liệu. Tuy nhiên, khi kích thước hoặc tính phức tạp của tập dữ liệu tăng lên, Redis sẽ tự động chuyển sang sử dụng skip list để đảm bảo hiệu quả hoạt động lâu dài. Bài viết về ziplist Trong phần trướckeo nha cai hom nay, chúng ta đã biết rằng ziplist là một khối bộ nhớ liên tục chứa nhiều mục dữ liệu. Vì mỗi phần tử của tập hợp đã sắp xếp (sorted set) đều bao gồm cả dữ liệu và điểm số (score), nên khi sử dụng lệnh zadd để thêm một cặp (dữ liệu, điểm số) vào bên trong, cơ chế dưới lớp sẽ chèn hai mục riêng biệt vào ziplist tương ứng: dữ liệu sẽ được đặt trước, còn điểm số sẽ đứng sau.

Điểm nổi bật chính của ziplist là khả năng tiết kiệm bộ nhớ đáng kểđá gà trực tiếp app, nhưng thao tác tìm kiếm trên nó chỉ có thể thực hiện theo thứ tự (có thể từ đầu đến cuối hoặc ngược lại). Do đó, các hoạt động truy vấn của sorted set sẽ thực hiện việc tìm kiếm tuần tự từ đầu đến cuối (hoặc ngược lại) trên ziplist, mỗi bước di chuyển sẽ bỏ qua hai phần tử dữ liệu, vượt qua một cặp (dữ liệu, điểm số). Trong quá trình này, thuật toán sẽ liên tục kiểm tra từng cặp giá trị và điểm số để xác định vị trí phù hợp, đảm bảo hiệu quả trong việc quản lý bộ nhớ mà vẫn duy trì được chức năng cơ bản củ Tuy nhiên, vì sự phụ thuộc vào thứ tự lưu trữ, cách tiếp cận này có thể trở nên kém hiệu quả hơn khi kích thước của ziplist tăng lên, dẫn đến thời gian tìm kiếm lâu hơn so với các cấu trúc dữ liệu khác.

Khi dữ liệu được chèn vàotỷ lệ kèo bóng đá trực tiếp, cấu trúc ziplist dưới đáy sorted set có thể sẽ chuyển đổi sang phiên bản thực hiện của zset (quá trình chuyển đổi chi tiết có thể tham khảo trong t_zset.c ở hàm zsetConvert). Vậy thì rốt cuộc cần chèn bao nhiêu phần tử thì mới xảy ra chuyển đổi?

Bạn còn nhớ hai cấu hình Redis được đề cập ở đầu bài không?

								
									zset-max-ziplist-entries 128
zset-max-ziplist-value 64

								

Cấu hình này có nghĩa là khi một trong hai điều kiện sau đây được đáp ứngđá gà trực tiếp app, ziplist sẽ được chuyển đổi thành zset (các điều kiện cụ thể có thể được tìm thấy trong t_zset.c, trong hàm zaddGenericCommand liên quan). Đây là cơ chế giúp tối ưu hóa việc quản lý dữ liệu trong trường hợp cần thiết.

• Khi số lượng phần tử trong tập hợp đã sắp xếp (sorted set) vượt quá 128tỷ lệ kèo bóng đá trực tiếp, tức là số lượng cặp dữ liệu (data, score) nhiều hơn 128, và đồng thời số lượng mục trong cấu trúc ziplist vượt quá 256, thì hệ thống sẽ tự động chuyển đổi sang một dạng biểu diễn khác để tối ưu hóa hiệu suất.
• Khi bất kỳ dữ liệu nào được chèn vào sorted set có chiều dài vượt quá 64.

Cuối cùngkeo nha cai hom nay, định nghĩa cấu trúc dữ liệu zset như sau:

								
									
										typedef
									 struct
									 zset
									 {
									
    dict
									 *
									dict
									;
									
    zskiplist
									 *
									zsl
									;
									
}
									 zset
									;
									

								

Tại sao Redis sử dụng skiplist mà không dùng cây cân bằng?

Redis được thiết kế để xử lý các yêu cầu nhanh chóng và hiệu quả trong môi trường phân tánkeo nha cai hom nay, vì vậy việc lựa chọn cấu trúc dữ liệu phù hợp là vô cùng quan trọng. Skiplist không chỉ cung cấp độ phức tạp thời gian trung bình O(log N) cho các hoạt động như tìm kiếm, chèn và xóa mà còn mang đến sự linh hoạt và khả năng mở rộng tốt hơn so với cây cân bằng. Đặc biệt, skiplist dễ triển khai hơn, giảm thiểu chi phí bảo trì và giúp tối ưu hóa hiệu suất tổng thể.

There are a few reasons:

1) They are not very memory intensive. It’s up to you basically. Changing parameters about the probability of a node to have a given number of levels will make then less memory intensive than btrees.

2) A sorted set is often target of many ZRANGE or ZREVRANGE operationstỷ lệ kèo bóng đá trực tiếp, that is, traversing the skip list as a linked list. With this operation the cache locality of skip lists is at least as good as with other kind of balanced trees.

3) They are simpler to implementđá gà trực tiếp app, debug, and so forth. For instance thanks to the skip list simplicity I received a patch (already in Redis master) with augmented skip lists implementing ZRANK in O(log(N)). It required little changes to the code.

Nguồn gốc của đoạn văn này:

https://news.ycombinator.com/item?id=1171423

Nguyên nhân được tóm tắt từ ba khía cạnh chính là mức sử dụng bộ nhớtỷ lệ kèo bóng đá trực tiếp, khả năng hỗ trợ tìm kiếm phạm vi và độ dễ dàng khi triển khai, những vấn đề này chúng ta thực tế đã đề cập đến ở phần trước. Ngoài ra, có thể thấy rằng mỗi yếu tố này đều đóng vai trò quan trọng trong việc lựa chọn phương án tối ưu, chẳng hạn như khi xử lý dữ liệu lớn, việc tối ưu hóa bộ nhớ không chỉ giúp cải thiện hiệu suất mà còn tạo nền tảng vững chắc cho các thao tác tiếp theo.

Trong phần tiếp theo của loạt bài nàykeo nha cai hom nay, chúng ta sẽ cùng tìm hiểu về intset và mối liên hệ của nó với kiểu dữ liệu set mà Redis cung cấp cho người dùng. Hãy cùng đón chờ những chia sẻ thú vị sắp tới nhé!

(Kết thúc)

Các bài viết được chọn lọc khác ：

• Phân tích sâu cấu trúc dữ liệu nội bộ của Redis (5) —— quicklist
• Phân tích sâu cấu trúc dữ liệu nội bộ của Redis (4) —— ziplist
• Phân tích sâu cấu trúc dữ liệu nội bộ của Redis (3) —— robj
• Phân tích sâu cấu trúc dữ liệu nội bộ của Redis (2) —— sds
• Phân tích sâu cấu trúc dữ liệu nội bộ của Redis (1) —— dict
• Bạn có cần hiểu công nghệ học sâu và mạng thần kinh không?
• Chính thống và dị đạo trong công nghệ
• Về sự chuyển biến trong cuộc đời
• Nguyên lý tăng entropy trong thế giới lập trình
• Push notification trên Android thực sự gây phiền phức đến mức nào?
• Xử lý bất đồng bộ trong Android và iOS (bốn) —— tác vụ và hàng đợi bất đồng bộ
• Quản lý số và dấu đỏ trong ứng dụng bằng mô hình cây