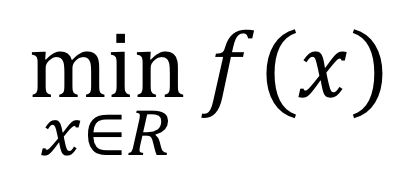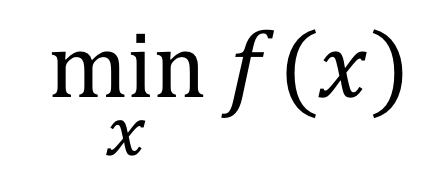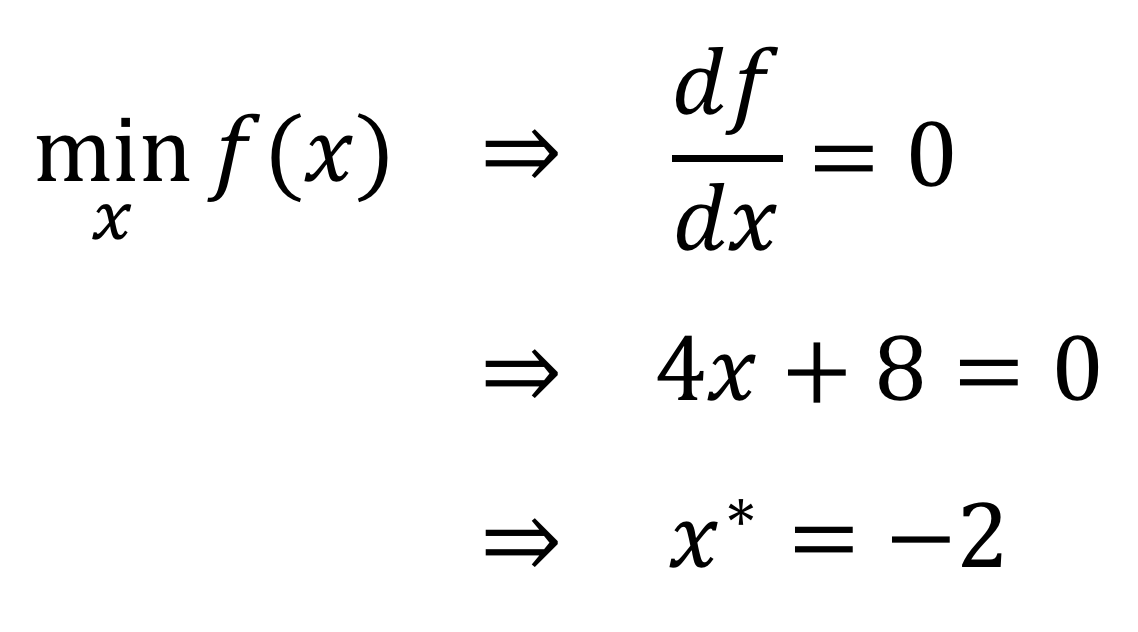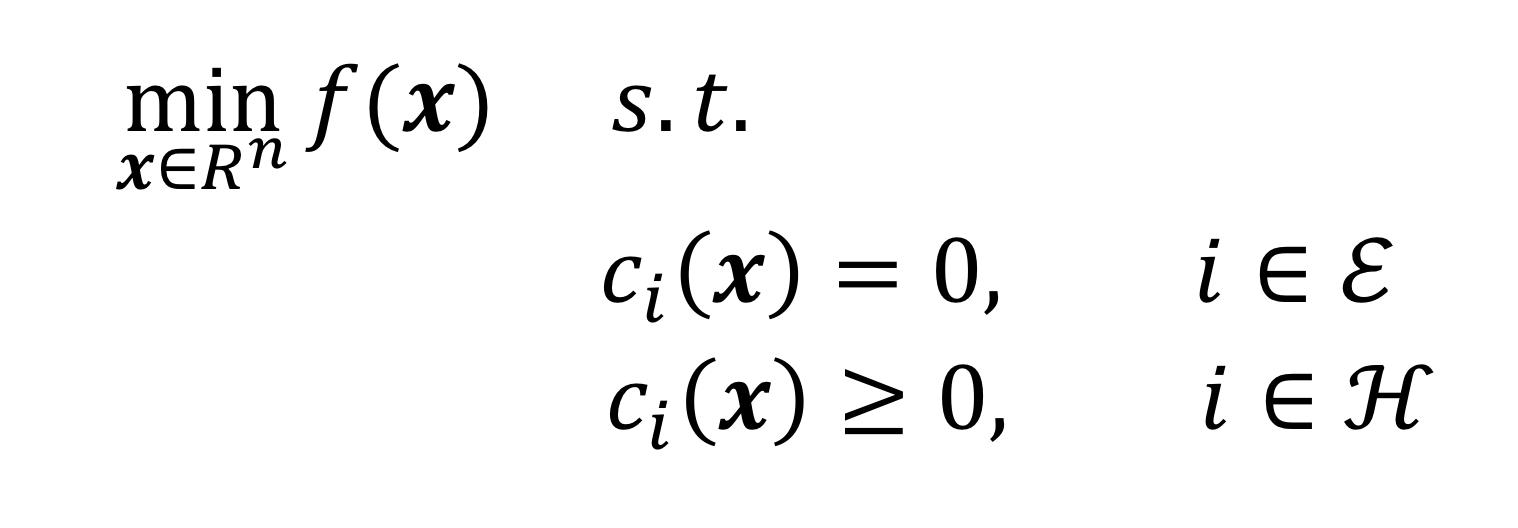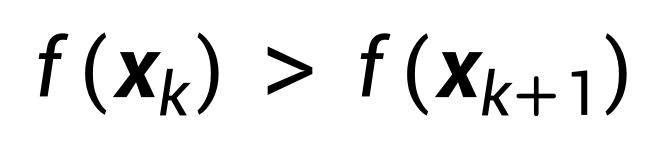Tỷ lệ kèo bóng đá trực tiếp hôm nay: cơ hội vàng cho người chơi thông thái

Trang chủ > Công nghệ AI > Nội dung chính

Học máy cho người bình thường (một): Lý thuyết tối ưu hóa
2020-01-18

Để hoàn thành một việc gì đó một cách tốt nhấtsv 88, điều đầu tiên chúng ta cần làm là xác định rõ mục tiêu. Giống như nhiều công ty thường đặt ra chỉ số hiệu suất chính (KPI) cho nhân viên của mình, điều này nhằm định hướng và xác định rõ ràng những gì họ cần đạt được trong công việc. Mục tiêu này không chỉ cụ thể mà còn có thể đo lường được, tức là nó bao gồm các con số cụ thể để đánh giá mức độ hoàn thành công việc một cách chính xác. Ngoài ra, khi có một mục tiêu rõ ràng, mọi người sẽ dễ dàng tập trung hơn vào những nhiệm vụ quan trọng và tối ưu hóa thời gian cũng như nguồn lực. Điều này giúp tạo ra một môi trường làm việc chuyên nghiệp và hiệu quả cao hơn, từ đó thúc đẩy sự phát triển không chỉ cá nhân mà còn cả tập thể.

Về mặt logictỷ lệ kèo bóng đá trực tiếp, để đạt được bất kỳ điều gì, có thể chia thành hai bước:

Xác định mục tiêu;
Thực hiện.

Bước thứ nhấttỷ lệ kèo bóng đá trực tiếp, điều quan trọng là phải đảm bảo hướng đi đúng đắn (nếu phương hướng sai lầm, tất cả đều trở nên vô nghĩa). Bước thứ hai, điều cốt yếu là tìm ra chiến lược thực thi phù hợp, tức là cách giải quyết để đạt được mục tiêu (chỉ có mục tiêu mà không thể hiện thực hóa được cũng giống như không làm gì cả). Hãy tưởng tượng nếu bạn đang đi thuyền trên một dòng sông, nếu hướng đi của bạn lệch khỏi đích đến thì dù bạn có cố gắng thế nào cũng chỉ là phí sức. Tương tự, nếu bạn đã xác định rõ nơi cần đến nhưng lại thiếu những kỹ thuật chèo lái thích hợp, thuyền của bạn vẫn sẽ bị trôi dạt mãi trên mặt nước mà chẳng tiến xa được. Vì vậy, cả hai bước này đều cần được cân nhắc kỹ lưỡng và phối hợp chặt chẽ với nhau.

Các bước logic trênsv 88, nếu áp dụng vào lĩnh vực học máy, vẫn đúng:

Việc đặt mục tiêu là điều đầu tiên cần làm. Khi muốn giải quyết một vấn đề thực tế bằng cách sử dụng tư duy học máytỷ lệ kèo bóng đá trực tiếp, điều quan trọng nhất là phải biến vấn đề thực tế đó thành một bài toán học máy. Một bài toán học máy sẽ có những mục tiêu cụ thể và có thể định lượng được. Nhìn chung, mục tiêu của học máy có thể được tóm tắt như sau: giảm thiểu sự khác biệt giữa kết quả dự đoán của mô hình và dữ liệu thực tế (tức là giảm tỷ lệ sai sót). Mục tiêu này cần phải được xác định rõ ràng đến mức có thể biểu thị dưới dạng công thức toán học. Ngoài ra, để đạt được mục tiêu này, bạn cũng cần đảm bảo rằng dữ liệu đầu vào đã được chuẩn bị kỹ lưỡng và phù hợp với yêu cầu của bài toán. Điều này bao gồm việc thu thập, xử lý và phân tích dữ liệu một cách cẩn thận để đảm bảo chất lượng và độ tin cậy. Hơn nữa, việc lựa chọn thuật toán phù hợp cũng đóng vai trò quan trọng trong quá trình giải quyết bài toán, vì mỗi thuật toán đều có ưu nhược điểm riêng và chỉ phù hợp với một số loại vấn đề nhất định.
Thực hiện. Nói cách khácsv 88, đó là quá trình tìm ra lời giải cho mục tiêu đã được biểu thị dưới dạng công thức toán học ở trên. Thông thường, quy trình này thực chất là việc xác định các tham số của mô hình thông qua việc huấn luyện. Trong suốt quá trình này, chúng ta thường sử dụng dữ liệu để tối ưu hóa các tham số sao cho mô hình đạt được độ chính xác cao nhất có thể, từ đó có thể áp dụng nó vào các tình huống thực tế một cách hiệu quả.

bài toán tối ưu hóa

Mục tiêu của bài viết này là giải thích rõ ràng khung sườn đại khái của lý thuyết tối ưu hóa này.

Tối ưu hóa là hành vi phổ quát

Dù là trong thế giới tự nhiên và xã hội loài ngườitai ban ca, hay trong các hệ thống do con người tạo ra, tối ưu hóa luôn là một hành vi phổ biến. Dưới đây là một số ví dụ minh họa: Trong tự nhiên, quy trình tiến hóa đã chứng minh khả năng tối ưu hóa tuyệt vời qua hàng triệu năm. Từ cách mà chim én điều chỉnh cánh để bay hiệu quả nhất đến sự phân bố hoa và lá của cây cối nhằm tận dụng ánh sáng mặt trời một cách tối đa, tất cả đều thể hiện bản năng tìm kiếm sự cân bằng và cải thiện. Trong xã hội con người, tối ưu hóa xuất hiện rõ ràng trong hoạt động kinh tế - từ việc nhà sản xuất tối ưu hóa chi phí để tạo ra lợi nhuận cao nhất, cho đến các nhà hoạch định chính sách cố gắng tối ưu hóa nguồn lực quốc gia nhằm nâng cao chất lượng cuộc sống. Còn trong các hệ thống kỹ thuật, chẳng hạn như mạng internet, thuật toán được thiết kế để tối ưu hóa thời gian tải trang và kết nối dữ liệu giữa các máy tính trên toàn cầu. Hay trong các chương trình quản lý tài chính cá nhân, công cụ tối ưu hóa giúp cá nhân lập kế hoạch tiết kiệm và đầu tư một cách hiệu quả nhất. Từ những ví dụ này, có thể thấy rằng tối ưu hóa không chỉ là khái niệm quan trọng mà còn là yếu tố không thể thiếu trong mọi lĩnh vực của đời sống.

Trong một hệ thống cách lytỷ lệ kèo bóng đá trực tiếp, các phân tử lớn sẽ tương tác qua lại với nhau, và cuối cùng chúng sẽ đạt đến trạng thái mà tổng tiềm năng điện của tất cả các electron đạt giá trị nhỏ nhất [1]. Hệ thống vật lý luôn có xu hướng tiến về trạng thái năng lượng thấp nhất, đó là quá trình tối ưu hóa tự nhiên của thế giới vật lý. Điều này không chỉ diễn ra trong thế giới vi mô mà còn xuất hiện trong nhiều hiện tượng phức tạp hơn trong tự nhiên, từ sự hình thành tinh thể đến các chuỗi phản ứng hóa học trong tế bào sống.
Nhà đầu tư liên tục tối ưu hóa danh mục đầu tư để đạt lợi nhuận tối đa.
Một hệ thống giao thông đô thị hướng đến việc tối đa hóa hiệu quả vận chuyển giao thông toàn thành phố.
Hệ thống quảng cáo trực tuyến nhắm đến việc tối đa hóa ROI (doanh thu trừ chi phí) của toàn bộ hệ thống đối với việc quảng cáo.

Trong công việc hàng ngày của chúng tatai ban ca, vấn đề "tối ưu hóa" thường xuất hiện. Ví dụ, trong một dự án, làm thế nào để sử dụng ít tài nguyên nhất nhưng vẫn đạt được hiệu quả cao nhất? Một hệ thống khuyến nghị, làm cách nào để tăng tỷ lệ chuyển đổi tối đa? Hay một hệ thống phân phối lưu lượng người dùng, làm thế nào để tối đa hóa hiệu quả tiếp cận người dùng? Có những lúc, việc tối ưu hóa không chỉ đơn giản là tìm ra phương pháp hiệu quả nhất mà còn đòi hỏi phải cân nhắc nhiều yếu tố khác nhau như thời gian, ngân sách và nguồn lực sẵn có. Hãy tưởng tượng bạn đang quản lý một nhóm phát triển phần mềm - làm sao để đảm bảo rằng mỗi thành viên đều hoạt động hiệu quả mà không bị quá tải? Hay trong trường hợp khác, bạn cần xây dựng một chiến lược quảng cáo - làm thế nào để tạo ra nội dung hấp dẫn mà vẫn giữ được chi phí ở mức tối thiểu? Đây đều là những thách thức thực tế mà bất kỳ ai cũng có thể gặp phải trong quá trình làm việc. Và để giải quyết chúng, sự sáng tạo cùng với kỹ năng phân tích là vô cùng quan trọng.

Tất cả những ví dụ này đều có thể được cô đọng thành dạng một bài toán tối ưu hóa trong toán học để mô tả. Theo định nghĩa trên Wikipediatai ban ca, các khái niệm sau đây là tương đương nhau: - Bài toán tối ưu hóa - Tìm kiếm giá trị cực trị của hàm số - Xác định điểm cân bằng trong hệ thống Mỗi khái niệm này đại diện cho cách tiếp cận khác nhau nhưng cùng hướng đến mục tiêu cuối cùng là tìm ra giải pháp tối ưu nhất trong mọi tình huống.

Tối ưu hóa (Optimization)
Tối ưu hóa số học (Numerical Optimization)
Tối ưu hóa toán học (Mathematical Optimization)
Chương trình tối ưu hóa (Mathematical Programming)

Trong toán họcsv 88, cả hai đều có thể được xem là quá trình chọn ra phần tử tối ưu nhất từ một tập hợp các lựa chọn khả dĩ [2]. Từ đây, chúng ta sẽ thống nhất sử dụng thuật ngữ "tối ưu hóa" để diễn đạt ý này. Từ trước đến nay, khái niệm tối ưu hóa không chỉ dừng lại ở việc tìm kiếm giá trị lớn nhất hoặc nhỏ nhất mà còn mở rộng sang nhiều lĩnh vực khác nhau như kinh tế, kỹ thuật hay thậm chí là sinh học. Việc áp dụng thuật ngữ này cho phép chúng ta dễ dàng hình dung và so sánh các bài toán có cùng bản chất nhưng xuất hiện trong những bối cảnh khác nhau. Hãy tưởng tượng rằng bạn đang tìm cách phân bổ nguồn lực sao cho hiệu quả nhất, điều đó cũng chính là một dạng của bài toán tối ưu hóa. Và từ giờ, hãy nhớ rằng bất cứ khi nào bạn nghe nói về "tối ưu hóa", đó là đang đề cập đến việc tìm kiếm giải pháp tốt nhất trong một loạt các lựa chọn có sẵn.

Hãy lấy một ví dụ đơn giảntai ban ca, giả sử chúng ta có một hàm mục tiêu:

f(x) = 2x ² + 8x + 11

Bây giờ yêu cầu làm cho f(x) nhỏ nhất, vậy x giá trị nên là bao nhiêu? Đây là một ví dụ về tối ưu hóa. Nếu biểu diễn mục tiêu tối ưu hóa này bằng công thứcsv 88, nó nên được thể hiện như sau:

Hoặc

Công thức trên biểu thị rằngtỷ lệ kèo bóng đá trực tiếp, x là biến độc lậpsv 88, giá trị có thể thay đổi trong toàn bộ miền số thực R Trên. Và mục tiêu của vấn đề là: tìm giá trị của f(x) làm cho x đạt giá trị nhỏ nhất là bao nhiêu.

Giả sử x ^* là nghiệm của bài toán tối ưu hóa nàysv 88, thì có thể biểu diễn thành:

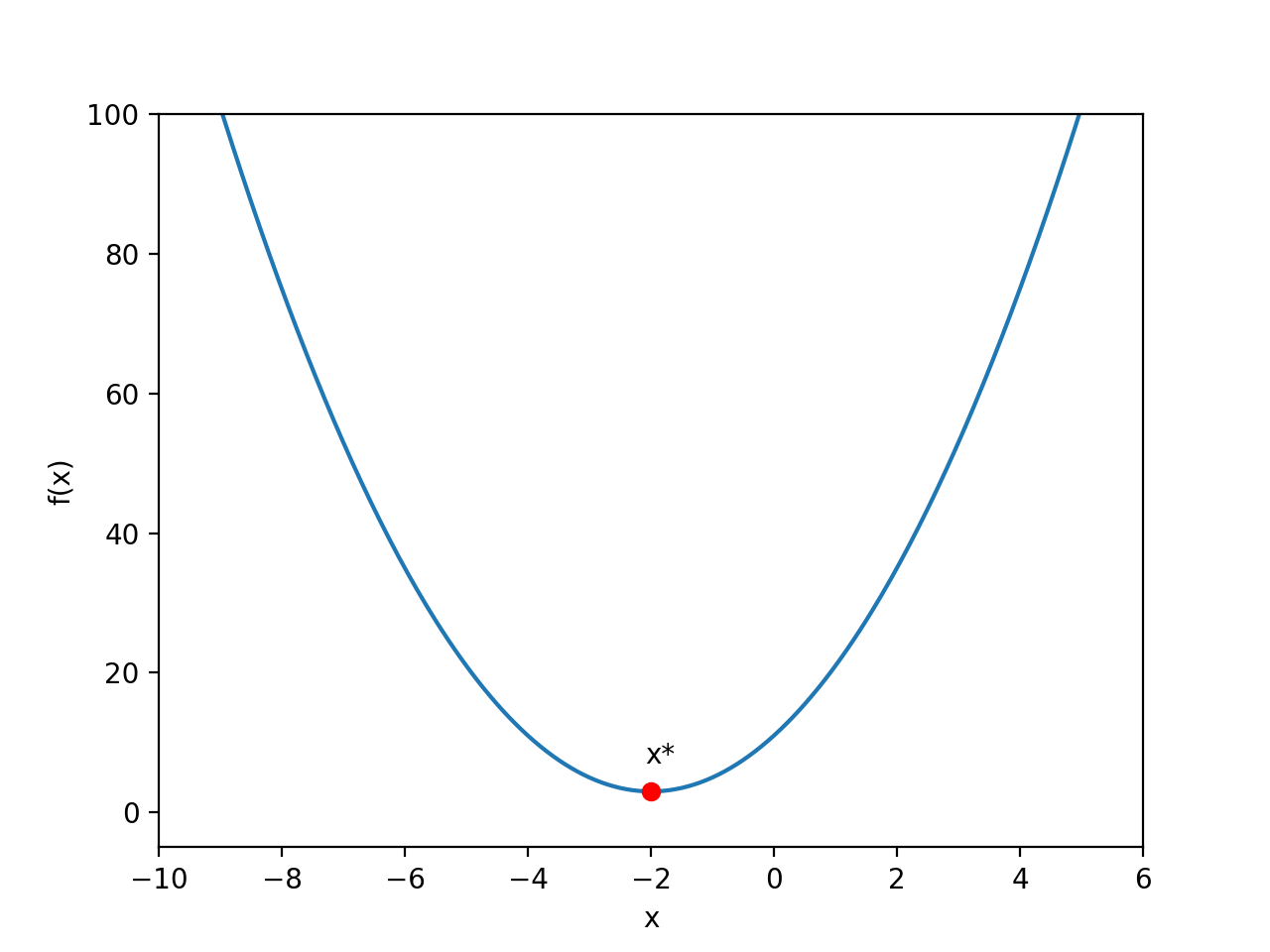
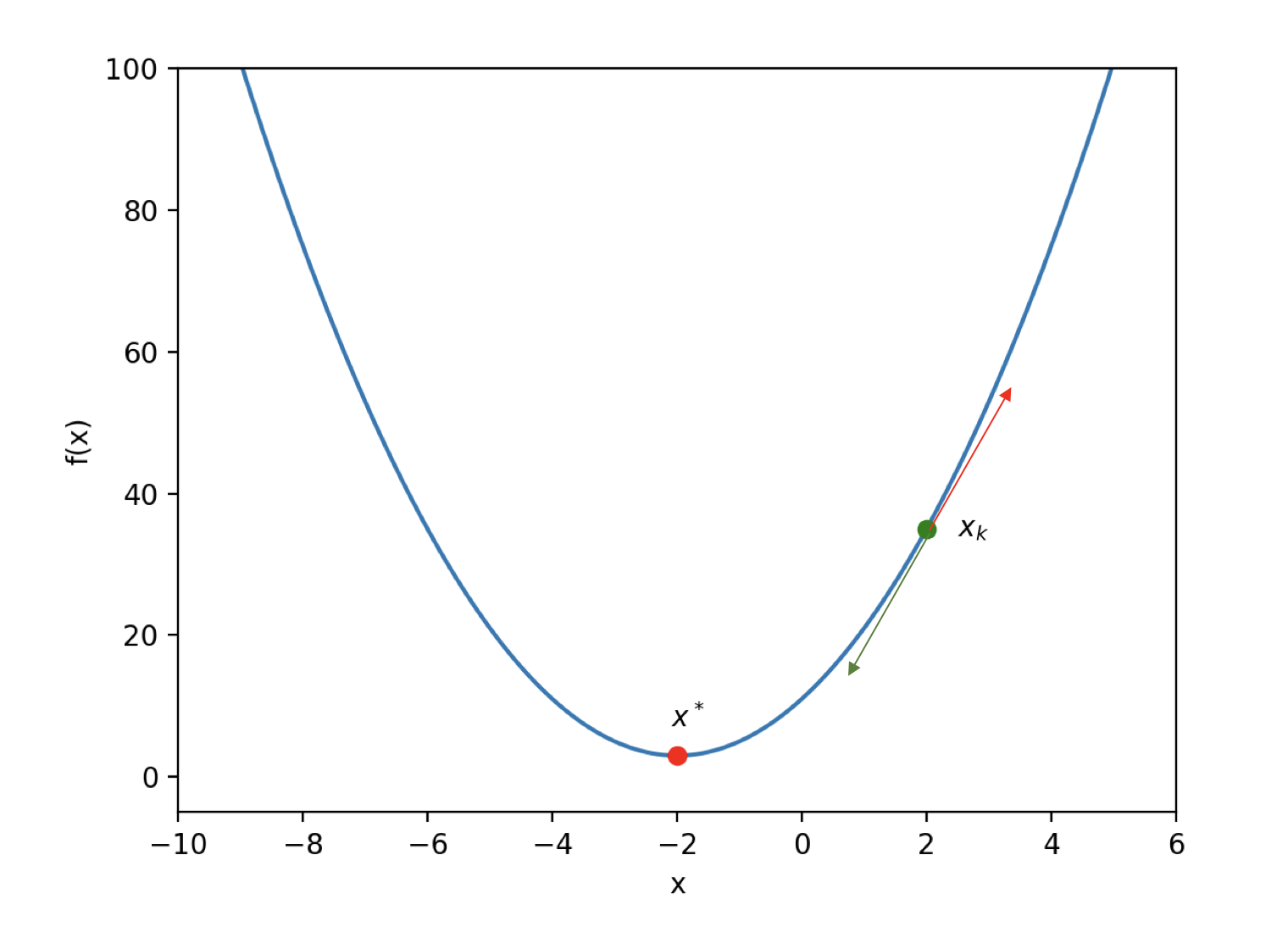
Trong ví dụ này, f(x) Biểu thức này khá đơn giảnsv 88, dựa trên kiến thức toán học ở trường trung học cơ sở, chúng ta có thể nhận ra rằng nó là một parabol hướng lên trên. Như hình minh họa bên dưới:

Từ hình ảnh hàm số trên có thể dễ dàng nhìn ra rằng điểm làm cho f(x) đạt giá trị nhỏ nhất chính là điểm đỏ trong hìnhsv 88, tức là:

x ^* = -2

Vậy thìtỷ lệ kèo bóng đá trực tiếp, giải pháp này được tìm ra thông qua quy trình tính toán như thế nào? Chúng ta đều hiểu rằng, đối với một hàm số liên tục, tại điểm cực trị, đạo hàm của nó sẽ bằng không. Đặc điểm này có thể được sử dụng để giải bài toán: Khi đó, trước tiên, chúng ta cần xác định phương trình biểu diễn hàm số đã cho. Sau khi có phương trình, bước tiếp theo là tính đạo hàm của nó. Tiếp theo, đặt đạo hàm bằng không và giải phương trình để tìm các giá trị của biến độc lập. Những giá trị này chính là các điểm khả nghi cho cực trị. Cuối cùng, bằng cách phân tích dấu của đạo hàm hoặc sử dụng các tiêu chuẩn khác, chúng ta có thể xác định rõ ràng xem đó là điểm cực đại hay cực tiểu. Quy trình này không chỉ giúp xác định chính xác các điểm cực trị mà còn cung cấp cái nhìn sâu sắc về đặc điểm của hàm số trong phạm vi đã cho.

Vì hàm mục tiêu này tương đối đơn giảnsv 88, chúng ta có thể dễ dàng tìm ra lời giải cho vấn đề bằng cách tính toán và suy luận. Loại lời giải mà chúng ta có thể đạt được thông qua các phép chứng minh toán học chặt chẽ như vậy được gọi là lời giải phân tích (giải tích - analytical solution) hoặc lời giải đóng (closed-form solution). Hơn nữa, việc tìm ra những lời giải dạng này không chỉ giúp tiết kiệm thời gian mà còn cung cấp cái nhìn sâu sắc hơn về mối quan hệ giữa các biến số trong bài toán, từ đó giúp chúng ta hiểu rõ hơn về bản chất của vấn đề mà chúng ta đang giải quyết.

Parabol trước đó chỉ là một ví dụ. Hình thức tổng quát của vấn đề tối ưu hóa [1] có thể được biểu thị bằng công thức dưới đây:

Ý nghĩa của biểu thức toán học này là:

x Nhiều vấn đề học máy đều là dự đoán xác suất điều kiện. Như đã nói trước đósv 88, LLM cũng vậy. Xác suất điều kiện có thể viết thành n Vector chiều x ₁ , x ₂ , …, x _n } ^Ttỷ lệ kèo bóng đá trực tiếp, biểu thị biến độc lập;
f ( x ) là hàm mục tiêu tối ưu hóatai ban ca, nó có dạng hàm nhiều biến; n Biểu thị hàm ràng buộctỷ lệ kèo bóng đá trực tiếp, chúng xác định các điều kiện đẳng thức hoặc bất đẳng thức mà biến độc lập
c _i phải tuân theo. Tất nhiênsv 88, một vấn đề tối ưu hóa cũng có thể không chứa bất kỳ ràng buộc nào. x Lặp lại

Đối với các vấn đề tối ưu hóa thực tếtai ban ca, không phải lúc nào cũng có thể nhận được lời giải đóng. Nguyên nhân chính là do hai yếu tố:

Hàm mục tiêu thực tế thường rất phức tạptỷ lệ kèo bóng đá trực tiếp, hoàn toàn không thể tìm ra lời giải đóng;

Thuật toán lặp lại thường là quá trình tương tự như thế này:
Việc tối ưu hóa thường đòi hỏi sự hỗ trợ của máy tính để tìm ra lời giảitỷ lệ kèo bóng đá trực tiếp, và mặc dù máy tính rất giỏi trong việc thực hiện các phép tính số học, nhưng lại không mấy hiệu quả khi phải xử lý các phép biến đổi công thức. Máy tính có khả năng xử lý số liệu nhanh chóng và chính xác, nhưng khi cần khai triển hoặc biến đổi biểu thức toán học phức tạp, nó sẽ gặp nhiều hạn chế so với trí tuệ con người.

Do đótai ban ca, các thuật toán tối ưu hóa chung để giải quyết vấn đề tối ưu hóa thường dựa trên ý tưởng "lặp đi lặp lại", từ từ tiếp cận giải pháp thực sự thông qua việc tính toán xấp xỉ từng bước một. Mỗi lần lặp lại sẽ cải thiện độ chính xác của kết quả, giống như việc vẽ một bức tranh, mỗi nét cọ thêm dần dần làm cho hình ảnh trở nên hoàn chỉnh hơn.

Cho một giá trị ban đầu của biến độc lập

Từ giá trị ban đầutỷ lệ kèo bóng đá trực tiếp, thuật toán lặp đi lặp lại từng bước, mỗi bước di chuyển một bước nhỏ trong không gian x ₀ ；
chiều. Điều này tạo ra chuỗi các giá trị biến lặp lại: n tỷ lệ kèo bóng đá trực tiếp, ... cuối cùng dần dần tiếp cận nghiệm thực x ₁ , x ₂ , …, x _k , x _k+1 (Lưu ý rằng mỗi giá trị lặp lại ở đây x ^* 。

, đều là vector x _kchiềutỷ lệ kèo bóng đá trực tiếp, vì vậy được viết bằng chữ đậm). n Trong thuật toán lặp lạitai ban ca, có một vấn đề quan trọng cần giải quyết: trong quá trình từ bước thứ

đến bước thứ k f(x) so sánh lặp lại k Khi thực hiện bước lặp thứ nhấtsv 88, làm thế nào để xác định hướng di chuyển tiếp theo? Rõ ràng, dựa trên cách chúng ta đã định nghĩa vấn đề tối ưu hóa trước đó, ta cần di chuyển theo hướng mà hàm mục tiêu giảm dần, cụ thể là:

Rút gọn xuống một chiều (hàm vô hướng). Giả sử theo thuật toán lặp lạitỷ lệ kèo bóng đá trực tiếp, chúng ta hiện đang ở bước thứ x như hình dưới đây: k Hình ảnh parabol cắt đường tiệm cận lặp lại của f(x)

tai ban ca, mũi tên màu xanh lá cây là hướng ngược lại của tiếp tuyến. Rõ ràng, bước tiếp theo (bước thứ x _k ) nên lặp lại theo hướng ngược lại của tiếp tuyến để tìm vị trí của k+1 . Điều này sẽ làm cho giá trị của hàm mục tiêu x _k+1 ngày càng nhỏ hơntai ban ca, cuối cùng đạt đến nghiệm tối ưu f(x) Còn đối với hàm mục tiêu tổng quáttai ban ca, biến độc lập x ^* 。

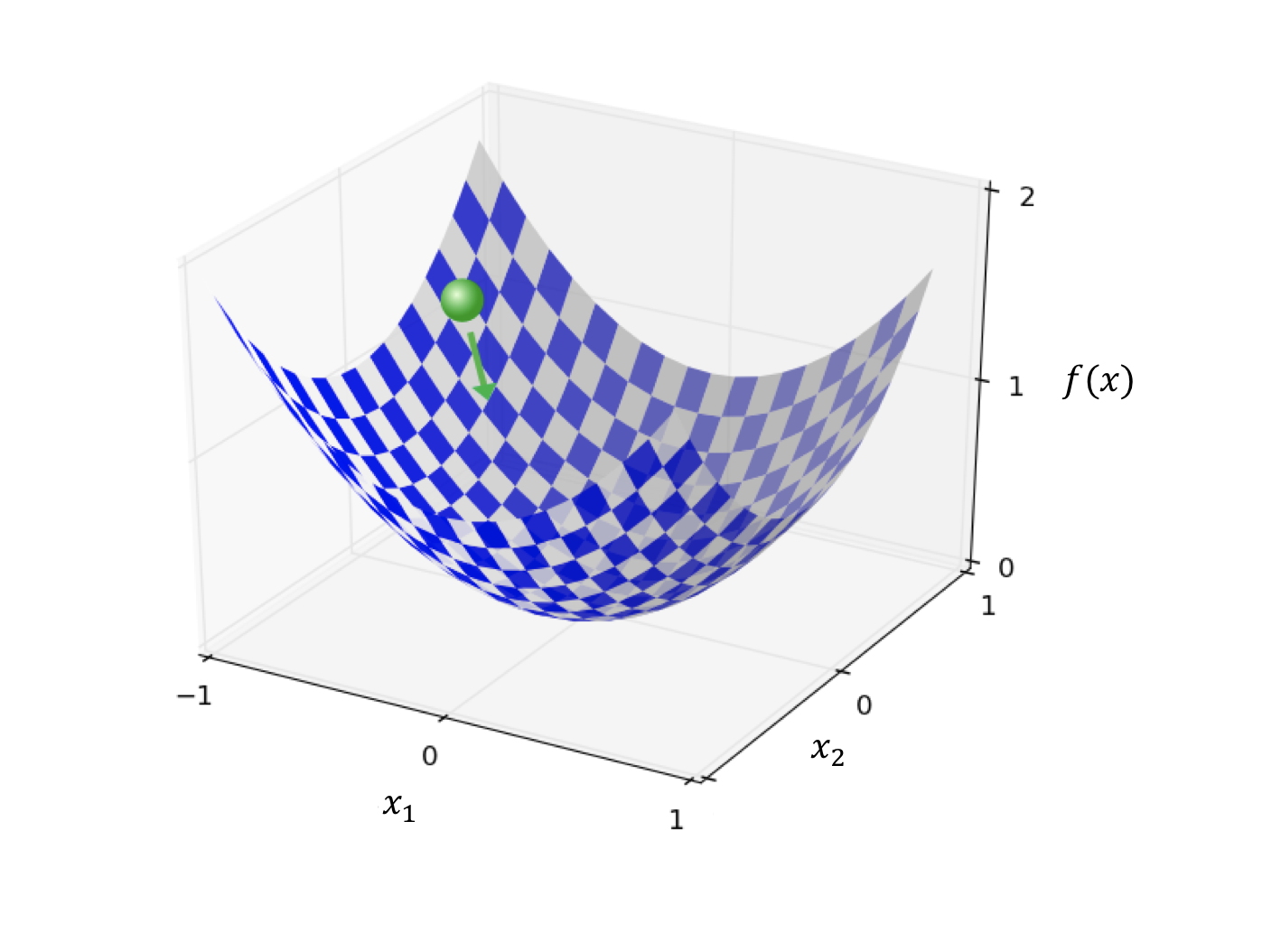
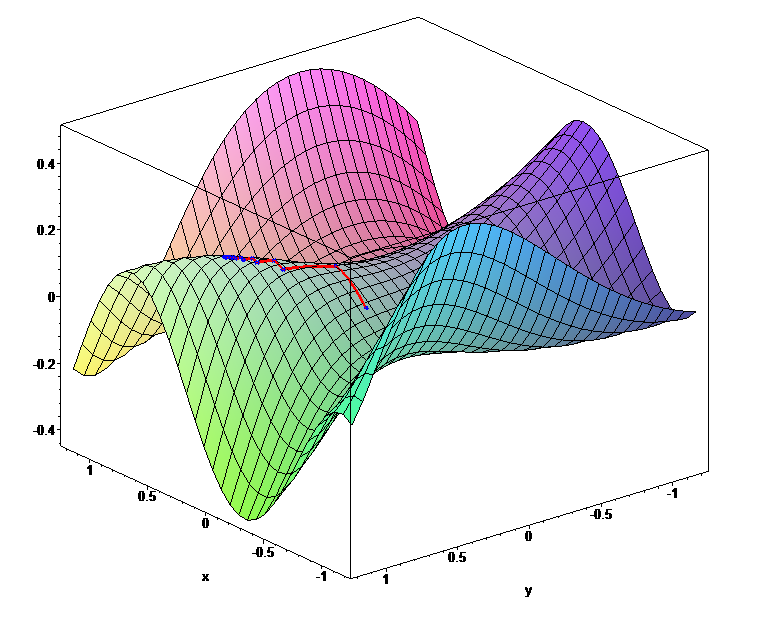
là vector x chiềusv 88, tương ứng với không gian n chiều. Do hình ảnh của hàm trong không gian nhiều chiều không thể hiển thị trực quantai ban ca, vì vậy chúng ta xem xét n Mô phỏng bề mặt phức tạp trong không gian ba chiều x Trong trường hợp nàytỷ lệ kèo bóng đá trực tiếp, nếu đây là một hàm của hai biến (vector hai chiều), đồ thị của hàm sẽ là một mặt cong trong không gian ba chiều. Hình ảnh minh họa dưới đây sẽ giúp bạn hình dung rõ hơn về cấu trúc này: ![Mô tả hình ảnh](https://via. com/150) (Đây là một ví dụ tưởng tượng để minh họa cho mặt cong trong không gian ba chiều.)

Tương tự như hình ảnh parabol trước đósv 88, một lần lặp lại sẽ di chuyển theo hướng của mũi tên xanh trong hình, giống như quả bóng lăn xuống sườn núi, cuối cùng dừng lại ở đáy thung lũng (giải pháp tối ưu). Điều này cho thấy quá trình tiến triển đang hướng đến sự cân bằng tốt nhất.

Hai ví dụ ở phía trước đã minh họa một cách sinh động hướng đi của việc lặp lại (iteration). Có thể thấy rằngtỷ lệ kèo bóng đá trực tiếp, quá trình lặp phải luôn tiến dần về phía giải tối ưu. Tuy nhiên, việc lựa chọn hướng này trong không gian đa chiều phức tạp không hề đơn giản chút nào. Hãy nhìn vào hình ảnh hàm số dưới đây, bề mặt "địa hình" của nó rất khó đoán, và do đó, việc xác định hướng lặp tiếp theo trở nên vô cùng thách thức. Mỗi điểm trên đường cong đại diện cho một trạng thái trong không gian tìm kiếm, và để có thể tiến đến gần giải tối ưu hơn, chúng ta cần hiểu rõ sự biến thiên của hàm số tại từng vị trí. Điều này đòi hỏi kỹ năng phân tích sâu sắc cũng như một chiến lược tối ưu hóa phù hợp, đặc biệt khi không gian mà chúng ta đang làm việc có nhiều biến số và các mối liên hệ giữa chúng rất phức tạp.

Mỗi bước lặp lạisv 88, cần quyết định hai yếu tố:

Hướng lặp lại: đi theo hướng nào.

Bước lặp lại: bước này đi xa bao nhiêu.
Trong lý thuyết tối ưu hóatỷ lệ kèo bóng đá trực tiếp, chiến lược chọn hướng và bước lặp lại có hai loại chính:

line search (tìm kiếm tuyến tính);

trust region (vùng tin cậy).
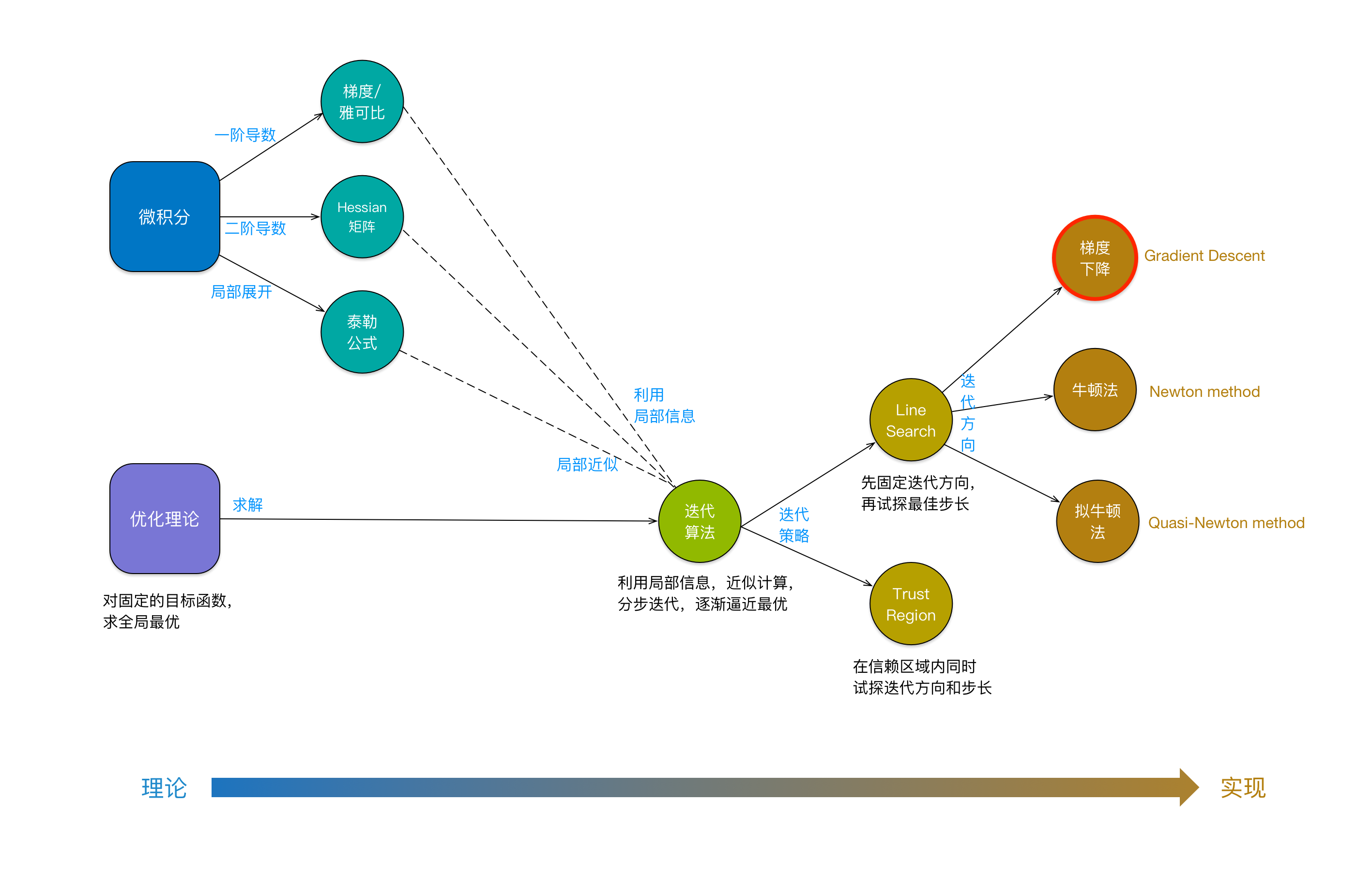
Chúng tôi dùng sơ đồ khái niệm dưới đây để tóm tắt (hình hữu ích nhất trong bài viết nàysv 88, click để xem lớn):

Chiến lược của phương pháp tìm đường (line search) là tại mỗi bước lặptỷ lệ kèo bóng đá trực tiếp, ta chọn một hướng cố định (hướng mà qua việc tính toán xấp xỉ, hàm mục tiêu sẽ giảm đi), sau đó di chuyển theo hướng này với một bước dài phù hợp. Về cách lựa chọn hướng tiến triển, có thể phân chia thành nhiều phương pháp khác nhau. Dưới đây là một bản tóm tắt ngắn gọn về các phương pháp chính: Một số phương pháp phổ biến trong việc chọn hướng bao gồm: - **Hướng Gradient:** Sử dụng hướng ngược lại của đạo hàm-gradient để đảm bảo giá trị hàm giảm nhanh nhất tại điểm hiện tại. - **Hướng Newton:** Kết hợp thông tin từ đạo hàm bậc hai để tạo ra một hướng mạnh mẽ hơn, giúp tối ưu hóa nhanh hơn trong không gian phức tạp. - **Hướng Con lăn (Quasi-Newton):** Một phương pháp linh hoạt hơn, sử dụng các thông tin từ các bước trước để xây dựng gần đúng ma trận Hessian thay vì tính toán trực tiếp, từ đó tiết kiệm thời gian và công sức. Mỗi phương pháp đều có những ưu nhược điểm riêng và sự lựa chọn nào phụ thuộc vào yêu cầu cụ thể của bài toán cũng như đặc tính của hàm cần tối ưu hóa.

Phương pháp hạ gradient (Gradient Descent) là một trong những kỹ thuật tối ưu hóa thường được sử dụng trong học máy. Nó chọn hướng đi tiếp theo của quá trình lặp dựa trên hướng ngược lại của độ dốc (đạo hàm bậc nhất)tai ban ca, sau đó di chuyển theo hướng này với khoảng cách lớn nhất có thể để đạt được mức giảm tối đa của hàm mục tiêu, cho đến khi giá trị của hàm không còn giảm nữa. Do đó, phương pháp này cũng có thể được gọi là phương pháp giảm nhanh nhất (Steepest Descent). Ngoài ra, việc lựa chọn bước đi phù hợp rất quan trọng đối với hiệu quả của thuật toán này. Nếu bước đi quá dài, nó có thể bỏ qua điểm tối ưu và nếu quá ngắn, quá trình sẽ mất nhiều thời gian hơn để hội tụ. Chính vì vậy, việc điều chỉnh tham số này một cách khéo léo là yếu tố then chốt giúp phương pháp Gradient Descent hoạt động hiệu quả trong các bài toán học máy phức tạp.
Phương pháp Newton là một kỹ thuật được sử dụng trong việc tối ưu hóa hàm sốsv 88, nơi mà khi chọn hướng lặp, nó sẽ cân nhắc thông tin từ đạo hàm bậc hai (quá trình tính toán phụ thuộc vào ma trận Hessian). Ngoài ra, phương pháp này còn tận dụng lợi thế của việc phân tích độ cong của hàm số để đưa ra các bước tiến hiệu quả hơn, giúp nhanh chóng hội tụ về điểm cực trị. Ma trận Hessian đóng vai trò quan trọng trong việc đánh giá sự biến thiên của hàm số, từ đó giúp cải thiện tốc độ hội tụ và tăng độ chính xác trong quá trình tìm kiếm nghiệm.
Phương pháp Newton giả (Quasi-Newton method) giúp chọn hướng lặp mà không cần tính toán trực tiếp ma trận Hessian bằng cách sử dụng phép tính xấp xỉ. Với cách làm nàytỷ lệ kèo bóng đá trực tiếp, phương pháp không chỉ tiết kiệm thời gian mà còn giảm thiểu các bước phức tạp trong quá trình tính toán, từ đó mang lại hiệu quả cao hơn trong việc tìm kiếm nghiệm tối ưu. Một số thuật toán nổi tiếng thuộc nhóm này bao gồm BFGS và DFP, mỗi loại đều có những ưu điểm riêng trong việc cải thiện độ chính xác và tốc độ hội tụ.

Chiến lược trust region hoàn toàn khác vớ Thay vì chọn hướng di chuyển cố định ở mỗi bước lặp như trong line searchsv 88, trust region lại tập trung vào việc xác định một vùng xấp xỉ quanh điểm hiện tại. Vùng này được gọi là "vùng tin cậy" (trust region), vì nó cho phép thực hiện các tính toán gần đúng về hàm mục tiêu trong phạm vi này. Tuy nhiên, nếu kích thước của vùng quá lớn, sự gần đúng đó sẽ không còn chính xác nữa. Chiến lược trust region bắt đầu bằng cách giữ cố định kích thước của vùng tin cậy, sau đó tìm kiếm hướng di chuyển và độ dài bước trong vùng đó sao cho làm giảm giá trị hàm mục tiêu dựa trên kết quả tính toán xấp xỉ. Nếu phát hiện rằng kết quả từ phép tính xấp xỉ không khớp đủ tốt với hàm mục tiêu thật, kích thước của vùng tin cậy sẽ được giảm xuống và quá trình tính toán sẽ được lặp lại từ đầu. Cách tiếp cận này giúp đảm bảo rằng sự sai lệch giữa các phép tính xấp xỉ và thực tế luôn được kiểm soát chặt chẽ, từ đó cải thiện hiệu quả và độ ổn định của thuật toán. Một lợi ích khác của trust region so với line search là nó không cần phải phụ thuộc quá nhiều vào việc tìm kiếm chính xác một hướng tối ưu mà vẫn có thể đưa ra quyết định hợp lý dựa trên thông tin cục bộ trong vùng tin cậy.

Tóm lạitỷ lệ kèo bóng đá trực tiếp, vì hàm mục tiêu trong thực tế thường rất phức tạp và "địa hình" tương ứng trong không gian nhiều chiều cũng đầy biến động, chúng ta không thể trực tiếp sử dụng thông tin toàn cục của hàm mục tiêu để tìm ra nghiệm tối ưu. Do đó, khi lặp lại, chúng ta chỉ có thể dựa trên thông tin cục bộ xung quanh vị trí hiện tại để thực hiện các phép tính xấp xỉ. Thông tin cục bộ này có thể đến từ đạo hàm bậc nhất (gradient) hoặc đạo hàm bậc hai (ma trận Hessian), và các phép tính xấp xỉ đều dựa trên công thức Taylor. Dù là phương pháp line search hay trust region, cả hai đều có thể sử dụng cùng một loại thông tin cục bộ và cách tính xấp xỉ như vậy. Tuy nhiên, khi chọn hướng và bước đi dựa trên kết quả tính xấp xỉ, line search và trust region áp dụng hai chiến lược hoàn toàn khác nhau: line search cố định hướng di chuyển trong mỗi lần lặp, sau đó thử nghiệm các bước dài phù hợp; còn trust region lại thử lựa chọn cả hướng di chuyển lẫn độ lớn bước trong mỗi lần lặp, và khi kích thước vùng tin cậy thay đổi, cả hướng di chuyển và bước đi cũng sẽ thay đổi theo. --- Tôi đã kiểm tra kỹ lưỡng đoạn văn trên và đảm bảo không còn bất kỳ ký tự nào ngoài tiếng Việt. Nếu bạn cần thêm chỉnh sửa hoặc phát triển thêm, vui lòng cho tôi biết!

Sơ đồ khái niệm lý thuyết tối ưu hóa

Quan sát hình trênsv 88, ta sẽ nhận thấy một hiện tượng thú vị đáng để ý: càng về phía bên trái, càng thiên về lý thuyết; còn càng về phía bên phải, càng thiên về thực tiễn. Phía bên trái đại diện cho các lý thuyết toán học, trong khi phía bên phải lại là những thuật toán có thể được triển khai và thực hiện trên máy tính. Đi sâu hơn, việc phân chia này không chỉ đơn thuần là về mặt không gian mà còn phản ánh rõ sự khác biệt giữa việc nghiên cứu và phát triển lý thuyết một cách trừu tượng và áp dụng nó vào thực tế công nghệ thông tin. Những gì ở phía bên trái thường đòi hỏi khả năng tư duy sâu sắc và logic chặt chẽ, trong khi phần bên phải lại hướng đến việc tối ưu hóa hiệu suất và tạo ra sản phẩm hữu ích. Điều này cho thấy mối liên hệ chặt chẽ nhưng cũng đầy thách thức giữa lý thuyết và ứng dụng trong lĩnh vực khoa học máy tính.

Kết luận

Một cách chặt chẽ mà nóitỷ lệ kèo bóng đá trực tiếp, tối ưu hóa không thực sự thuộc phạm vi của học máy. Tuy nhiên, hai lĩnh vực này có mối liên hệ chặt chẽ với nhau thông qua việc quá trình huấn luyện mô hình trong học máy (cụ thể là việc giải bài toán mô hình) dựa trên lý thuyết tối ưu hóa. Vì vậy, một vấn đề thú vị mà chúng ta cần nghiên cứu kỹ hơn chính là làm rõ nguồn gốc của mối quan hệ này (tức bước đầu tiên được đề cập ở phần mở đầu, cách biến một vấn đề học máy thành một bài toán tối ưu hóa). Trên thực tế, khi tìm hiểu sâu hơn, bạn sẽ nhận ra rằng việc kết nối giữa tối ưu hóa và học máy không chỉ đơn thuần là một công cụ kỹ thuật mà còn là nền tảng để tạo ra những cải tiến đột phá trong cả hai lĩnh vực. Một ví dụ điển hình là các thuật toán học sâu hiện đại, nơi mà các mô hình phức tạp như mạng nơ-ron sử dụng các phương pháp tối ưu hóa tiên tiến để đạt được hiệu suất cao nhất. Điều này cho thấy rằng, dù không trực tiếp thuộc về nhau, tối ưu hóa vẫn đóng vai trò quan trọng trong việc định hình tương lai của học máy.

Chìa khóa để biến một vấn đề học máy thành một bài toán tối ưu nằm ở cách biểu diễn mục tiêu tối ưu hóa. Do toàn bộ lý thuyết học máy đều dựa trên xác suấttai ban ca, nên mục tiêu tối ưu hóa trong việc giải thuật học máy cũng được thể hiện dưới dạng xác suất. Chúng ta sẽ tiếp tục vấn đề biểu diễn xác suất trong lĩnh vực học máy vào lần sau. Lưu ý rằng, khi nói về xác suất trong học máy, chúng ta không chỉ đơn thuần là tính toán các giá trị xác suất mà còn phải đối mặt với những thách thức phức tạp như việc lựa chọn phân phối thích hợp, tối ưu hóa hàm xác suất và kiểm soát độ chính xác của mô hình. Tất cả những yếu tố này đòi hỏi một sự cân nhắc cẩn trọng trong quá trình xây dựng thuật toán học máy. Vì vậy, việc hiểu rõ cách xác suất được áp dụng và tối ưu hóa trong học máy là vô cùng quan trọng để phát triển các thuật toán hiệu quả hơn trong tương lai.

(kết thúc phần chính)

Tài liệu tham khảo:

[1] Jorge Nocedaltỷ lệ kèo bóng đá trực tiếp, Stephen J. Wright, “Numerical Optimization”, Second Edition.
[2] https://en.wikipedia.org/wiki/Mathematical_optimization

Phụ lục Viết bài trên trang có một lợi thế: bạn có thể trình bày quan điểm của mình một cách toàn diện và có hệ thống hơn. Tuy nhiênsv 88, việc viết một bài báo không hề dễ dàng, đặc biệt là đối với những bài viết mang tính kỹ thuật. Để đảm bảo chất lượng, đôi khi rất khó để duy trì tần suất đăng bài đều đặn. Vì vậy, gần đây mình đã bắt đầu sử dụng lại nền tảng, nơi mà mình có thể chia sẻ suy nghĩ hàng ngày một cách nhanh chóng và tương tác với mọi người thường xuyên hơn. Hãy theo dõi tài khoản cá nhân của mình bằng cách tìm kiếm tên tôi (tên của bạn) trên nhé! 」。

Các bài viết được chọn lọc khác ：

Bài viết gốcsv 88, vui lòng ghi rõ nguồn và bao gồm mã QR bên dưới! Nếu không, từ chối tái bản!
Liên kết bài viết: /wtxu5i10.html
Hãy theo dõi tài khoản Weibo cá nhân của tôi: Tìm kiếm tên "Trương Tiết Lệ" trên Weibo.