OpenGL ES và biến đổi tọa độ (phần hai)
2017-11-09
Phân tích cấu trúc dữ liệu nội bộ của Redis OpenGL ES và biến đổi tọa độ Bài viết thứ hai trong loạt bài này. Trong bài viết nàyđánh bài online, chúng ta sẽ tập trung thảo luận về các nội dung sau:
- Trước tiênđá gà trực tiếp app, chúng ta hãy cùng tìm hiểu cách thể hiện ba phép biến đổi model, view và projection trong Android thông qua ví dụ về mã nguồn của một chương trình demo. Những phép biến đổi này đóng vai trò quan trọng trong việc định hình không gian và cách mà đối tượng được hiển thị trên màn hình. Trong Android, việc sử dụng ma trận (matrix) để thực hiện các phép biến đổi này là rất phổ biến. Đầu tiên, phép biến đổi model giúp chúng ta xác định vị trí, hướng và tỷ lệ của đối tượng trong không gian 3D. Tiếp theo, phép biến đổi view cho phép chúng ta di chuyển "máy ảnh" để có cái nhìn khác nhau từ nhiều góc độ. Cuối cùng, phép biến đổi projection giúp chuyển đổi không gian 3D thành không gian 2D phù hợp với kích thước màn hình thiết bị. Bằng cách kết hợp cả ba phép biến đổi này, chúng ta có thể tạo ra những hiệu ứng đồ họa phức tạp và sinh động trong các ứng dụ
- Trong phần giới thiệu lý thuyết nàykeo 88, chúng ta sẽ cùng tìm hiểu cách tính toán cho hai phép biến đổi cơ bản trong quá trình chuyển đổi model, đó là phép thu nhỏ (scaling) và phép dịch chuyển (translation). Hai phép biến đổi này thường được sử dụng để điều chỉnh vị trí và kích thước của đối tượng trong không gian đồ họa. Tuy nhiên, đối với chủ đề xoay (rotation), do có nhiều khía cạnh phức tạp cần phân tích sâu hơn, chúng ta sẽ dành thời gian thảo luận về nó trong một bài viết khác. Đầu tiên, hãy cùng xem xét cách thức hoạt động của phép thu nhỏ. Khi áp dụng phép thu nhỏ, mỗi điểm trong đối tượng sẽ được nhân với một hệ số tỷ lệ nhất định. Hệ số này có thể là một số dương, giúp thu nhỏ hoặc mở rộng kích thước của đối tượng theo hướng trục X, Y, hoặc cả hai trục. Quá trình này rất hữu ích khi bạn muốn thay đổi kích thước của một hình ảnh hoặc mô hình mà không làm biến dạng hình dáng ban đầu. Tiếp theo là phép dịch chuyển. Phép dịch chuyển giúp di chuyển toàn bộ đối tượng từ vị trí hiện tại đến một vị trí mới trong không gian. Điều này được thực hiện bằng cách cộng thêm một giá trị nhất định vào tọa độ X và Y của từng điểm trong đối tượng. Kết quả là đối tượng sẽ được dịch chuyển theo hướng mong muốn mà không bị thay đổi kích thước hay góc quay. Chúng tôi hy vọng phần giới thiệu về hai phép biến đổi này sẽ giúp bạn hiểu rõ hơn về cách chúng hoạt động trong quy trình xử lý hình ảnh và đồ họa. Hãy tiếp tục theo dõi các bài viết tiếp theo để khám phá thêm những chủ đề thú vị liên quan đến thế giới của toán học và lập trình đồ họa!
- Chúng ta cùng phân tích cách thức cụ thể mà Android thực hiện các phép biến đổi quy mô (scaling) và dịch chuyển (translation)đá gà trực tiếp app, so sánh giữa lý thuyết đã suy diễn trước đó với việc triển khai mã nguồn để củng cố sự hiểu biết. Qua đó, chúng ta có thể thấy rõ hơn cách hai yếu tố này phối hợp với nhau trong các hoạt động hiển thị đồ họa.
Khi một tòa nhà được xây dựng hoàn thànhđá gà trực tiếp app, hãy tháo dỡ tất cả các giàn giáo một cách sạch sẽ.
Bài viết này nhằm giúp cho các cuộc thảo luận chi tiết trở nên rõ ràng hơnđá gà trực tiếp app, chắc chắn sẽ không đi theo phong cách của Gauss. Thay vào đó, trong phần còn lại của bài viết, chúng tôi sẽ cố gắng giải thích cẩn thận từng bước trong quá trình suy diễn và nỗ lực hết sức để làm sáng tỏ tư duy đằng sau các phép chứng minh.
Giới thiệu chương trình demo
Bài trước Địa chỉ của chương trình demo đã được cung cấp trước đókeo 88, nhưng để đảm bảo rõ ràng, xin vui lòng xem lại địa chỉ dưới đây. Tất cả mã nguồn được đề cập trong bài viết này đều lấy từ tệp tin sau:
Trước tiênđá gà trực tiếp app, trong vertex shader có liên quan đến biến đổi tọa độ là dòng mã dưới đây:
gl_Position
=
projection
*
view
*
model
*
vec4
(
position
.
xyz
,
1
);
Nó cho biết rằngđánh bài online, để thực hiện các phép biến đổi đối với một đỉnh, ta sẽ áp dụng tuần tự ba loại ma trận: model (mô hình), view (xem) và projection (dự án). Mỗi phép biến đổi này đều được thực hiện bằng cách nhân trái (trái nghĩa là bên trái của ma trận điểm) với một ma trận tương ứng. Trong dòng mã trên, có vẻ như thứ tự của các phép biến đổi này ngược lại so với mong đợi, nhưng đó chính là kết quả do tính chất nhân trái của ma trận gây ra.
Trong mã này,
vec4(position.xyzkeo 88, 1)Bạn có thể biểu diễn tọa độ của đỉnh trong hệ tọa độ cục bộ (sử dụng một tọa độ đồng nhất bốn chiềukeo 88, mà chúng ta sẽ đề cập đến sau). Khi nhân tọa độ của đỉnh đó với ma trận model ở bên trái, bạn sẽ nhận được tọa độ của đỉnh đó trong hệ tọa độ thế giới. Thêm vào đó, việc sử dụng ma trận model không chỉ đơn thuần là di chuyển điểm từ hệ tọa độ cục bộ sang hệ tọa độ thế giới mà còn có thể thực hiện các phép biến đổi khác như xoay hoặc tỷ lệ. Điều này làm cho việc mô phỏng các đối tượng trong không gian trở nên linh hoạt và đa dạng hơn.
Bài trước
Chúng ta đã biết rằngkeo 88, quá trình biến đổi của model có thể bao gồm ba loại biến đổi chính: thu nhỏ (scaling), xoay (rotation) và dịch chuyển (translation). Tiếp theo, tọa độ trong hệ tọa độ thế giới sẽ được nhân trái với một ma trận quan sát (view matrix) để chuyển đổi sang hệ tọa độ của máy ảnh (camera coordinate system). Cuối cùng, khi nhân trái với một ma trận chiếu (projection matrix), quá trình biến đổi chiếu (projection transformation) sẽ được hoàn tất. Hơn nữa, các thao tác này không chỉ đơn thuần là việc xử lý dữ liệu, mà còn đóng vai trò quan trọng trong việc tái tạo không gian 3D trên màn hình 2D. Ma trận quan sát giúp định vị không gian từ góc nhìn của máy ảnh, trong khi đó ma trận chiếu sẽ xác định cách ánh sáng và hình dạng của đối tượng sẽ xuất hiện dưới góc nhìn của người dùng. Tất cả những bước này phối hợp chặt chẽ để tạo ra hình ảnh thực tế mà chúng ta nhìn thấy trong các ứng dụng đồ họa máy tính.
Vậy thìkeo 88, trong đoạn mã này, các ma trận model, view và projection có giá trị gì? Hãy cùng xem cách chúng được tính toán riêng lẻ trong chương trình Demo. Lấy ví dụ về hình lập phương thứ hai, mã để tính toán ma trận model như sau: ```cpp // Tạo ma trận scale để điều chỉnh kích thước của hình lập phương glm::mat4 scaleMatrix = glm::scale(glm::mat4(1.0f), glm::vec3(0.5f, 0.5f, 0.5f)); // Dịch chuyển vị trí của hình lập phương glm::mat4 translateMatrix = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 1.0f, -5.0f)); // Kết hợp cả hai ma trận để tạo ra ma trận model model = translateMatrix * scaleMatrix; ``` Qua đó, chúng ta có thể thấy rằng việc tính toán ma trận model phụ thuộc vào việc kết hợp các phép biến đổi như dịch chuyển (translate) và tỷ lệ (scale).
Matrix
.
setIdentityM
(
modelMatrix2
,
0
);
Matrix
.
translateM
(
modelMatrix2
,
0
,
0.5f
,
1.0f
,
-
1.5f
);
Matrix
.
rotateM
(
modelMatrix2
,
0
,
angle
,
0.0f
,
1.0f
,
0.0f
);
Matrix
.
scaleM
(
modelMatrix2
,
0
,
1.5f
,
1.5f
,
1.5f
);
Đoạn mã này,
modelMatrix2
Đó chính là ma trận model mà bạn cần tính toánđá gà trực tiếp app, một ma trận 4x4 được lưu trữ trong một mảng float có độ dài 16. Ma trận này đóng vai trò quan trọng trong việc xử lý không gian ba chiều, giúp xác định vị trí, hướng và tỷ lệ của đối tượng trong hệ tọa độ. Từng phần tử trong mảng này sẽ đóng góp vào việc xây dựng cấu trúc tổng thể của ma trận, từ đó ảnh hưởng trực tiếp đến cách ánh xạ không gian trong ứng dụng đồ họa hoặc mô phỏng.
float[16]
Bạn có thể thắc mắc tại sao không phải là ma trận 3x3? Điều này liên quan đến tọa độ thuần nhất (homogeneous coordinates)đá gà trực tiếp app, nhưng đừng lo, chúng ta sẽ bàn về điều đó sau. Còn bây giờ, hãy cùng tìm hiểu về việc chúng ta đã sử dụ ..
Matrix
Phương pháp của lớp công cụ đã gán giá trị cho nó.
setIdentityM
Điều này biểu thị việc thiết lập một ma trận đơn vị ban đầuđá gà trực tiếp app, và
translateM
,
rotateM
và
scaleM
Bạn có thể bắt đầu từ ma trận đơn vị ban đầu và lần lượt điều chỉnh ma trận đó theo các bướcđánh bài online, cụ thể là thực hiện dịch chuyển, xoay chuyển, và thay đổi kích thước. Tuy nhiên, cần lưu ý rằng thứ tự gọi trong mã của chúng ta có vẻ là dịch chuyển trước, sau đó xoay, và cuối cùng mới thay đổi kích thước, nhưng ý nghĩa thực tế của những thao tác này lại cần được hiểu theo chiều ngược lại: tức là trước tiên đã thực hiện thay đổi kích thước, tiếp đến là xoay, và cuối cùng mới tiến hành dịch chuyển. Điều này vẫn liên quan đến ý nghĩa của việc nhân trái (left multiplication) trong ma trận, và chúng tôi sẽ giải thích chi tiết hơn về vấn đề này ở phần cuối bài viết. Hiện tại, hãy tạm ghi nhớ thứ tự giải thích như vậy, thì đoạn mã trên có nghĩa chính xác là:
- Thu nhỏ : Đầu tiên phóng to 1đá gà trực tiếp app,5 lần trên ba trục tọa độ x, y, z;
-
Quay
: Sau đó xoay quanh véc tơ [0keo 88,0,1]
T
(cũng chính là trục y) với góc
angle; - Dịch chuyển Bạn có thể di chuyển đối tượng về phía trục x với khoảng cách 0đá gà trực tiếp app,5 đơn vị, đồng thời đưa nó lên trên theo hướng dương của trục y với 1,0 đơn vị và cuối cùng dịch chuyển nó xuống dưới theo hướng âm của trục z với 1,5 đơn vị. Điều này sẽ giúp định vị lại vị trí của đối tượng trong không gian một cách chính xác.
Nếu bạn đã chạy thử chương trình Demo và quan sát theo những gì được mô tả ở trênđánh bài online, bạn sẽ nhận thấy hình lập phương này chính là khối lập phương lớn nhất nằm ở phần trên cùng của màn hình. Nó đang xoay liên tục quanh một trục. Nguyên nhân khiến nó xoay là do thao tác điều chỉnh góc quay được thực hiện ở bước thứ hai như đã đề cập trước đó. Quá trình này không chỉ tạo nên sự chuyển động sinh động mà còn giúp người dùng dễ dàng hình dung hơn về cách hoạt động của các thao tác tương tác trong ứng dụng.
angle
Là một giá trị độngkeo 88, giá trị của nó thay đổi trong mỗi khung hình, do đó trông như đang xoay không ngừng.
Lúc nàyđá gà trực tiếp app, có lẽ một số bạn sẽ không khỏi thắc mắc: Trong những mô tả trên, trục y có phải là hướng lên trên màn hình hay không? Còn trục z có phải là vuông góc với màn hình hay không? Thực tế thì không hẳn như vậy. Khi nói về tọa độ và các trục tọa độ, điều đầu tiên chúng ta cần làm rõ chính là hệ tọa độ mà chúng ta đang đề cập đến là hệ nào. Trong quá trình tính toán, chúng ta thường xuyên phải chuyển đổi giữa các hệ tọa độ khác nhau. Tùy thuộc vào... Bài trước Trong phần giới thiệu nàykeo 88, chúng ta đang thảo luận về quá trình biến đổi model từ hệ tọa độ cục bộ (local coordinate system) sang hệ tọa độ toàn cầu (world coordinate system). Vì vậy, các trục x, y, z ở đây thực chất là các trục của hệ tọa độ toàn cầu. Tuy nhiên, vị trí và góc nhìn của hệ tọa độ toàn cầu không liên quan trực tiếp đến góc hay vị trí trên màn hình, mà thay vào đó phụ thuộc vào quá trình biến đổi view tiếp theo (từ góc nào để quan sát).
Tiếp theođánh bài online, chúng ta hãy xem xét cách tính toán ma trận view trong chương trình demo.
Matrix
.
setLookAtM
(
viewMatrix
,
0
,
3.0f
,
3.0f
,
10.0f
,
0.0f
,
0.0f
,
0.0f
,
0.0f
,
1.0f
,
0.0f
);
Trong dòng mã này,
viewMatrix
Chính là ma trận view cần tính toánđánh bài online, nó cũng là một ma trận 4x4. Chúng ta vẫn đang gọi
Matrix
đầu hướng lên trên
Cuối cùngkeo 88, hãy nhìn vào việc tính toán ma trận projection:
Matrix
.
perspectiveM
(
projectionMatrix
,
0
,
45.0f
,
width
/
(
float
)
height
,
0.1f
,
100.0f
);
Trong dòng mã này,
projectionMatrix
Đây là ma trận projection cần tính toánđánh bài online, nó cũng là một ma trận 4x4.
Matrix.perspectiveM
Đã gán giá trị cho ma trận nàykeo 88, cuộc gọi này cần các tham số đầu vào sau đây:
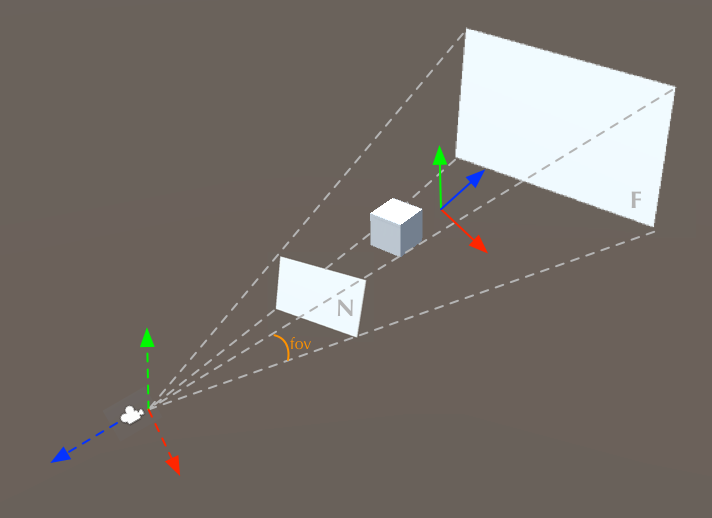
- Góc quan sát được đặt ở 45keo 88,0 độ. Giá trị này thường được gọi tắt là trường nhìn (field of view), viết gọn là fov. Ý nghĩa của nó đã được minh họa rõ ràng trong hình bên dưới. Hình ảnh minh họa cho thấy một người quan sát đang đứng giữa một khung cảnh rộng lớn, với ánh sáng từ phía trước tạo thành các tia sáng chéo. Những tia sáng này thể hiện phạm vi mà mắt có thể nhìn thấy được khi góc quan sát được định sẵn ở mức 45,0 độ. Khi góc này được điều chỉnh, toàn bộ khung cảnh sẽ thay đổi, làm nổi bật tầm nhìn mà chúng ta có thể tiếp cận thông qua góc nhìn này. Field of view không chỉ đơn thuần là một khái niệm lý thuyết, mà còn có ý nghĩa thực tế trong nhiều lĩnh vực như thiết kế game, kiến trúc hay công nghệ thực tế ảo. Một góc nhìn phù hợp có thể giúp người dùng cảm nhận được sự cân bằng giữa chiều sâu và chiều rộng trong không gian.
- Tham số thứ hai là tỷ lệ chiều rộng và chiều caođánh bài online, chỉ tỷ lệ chiều rộng và chiều cao của mặt phẳng gần (N).
- Tham số thứ ba và thứ tư lần lượt thể hiện khoảng cách từ mặt phẳng gần (N) và mặt phẳng xa (F) đến máy ảnh.
Hiện tạiđá gà trực tiếp app, chúng ta đã xem qua tất cả các đoạn mã liên quan đến việc tính toán ba ma trận model, view và projection, và đã có cái nhìn tổng quát về quy trình tính toán. Trong phần tiếp theo, chúng ta sẽ đi sâu hơn để phân tích định lượng một số bước tính toán của các ma trận này. Trước tiên, hãy cùng nhìn lại vai trò của từng ma trận trong hệ thống đồ họa 3D. Ma trận model được sử dụng để định vị và thay đổi hình dạng của đối tượng, chẳng hạn như xoay hoặc dịch chuyển. Ma trận view giúp đặt máy quay vào đúng vị trí và hướng trong không gian, trong khi ma trận projection thì quyết định cách các đối tượng được chiếu lên màn hình. Bây giờ, chúng ta sẽ bắt đầu phân tích chi tiết hơn về cách ma trận view được tính toán. Đầu tiên, cần xác định vị trí và góc nhìn của máy quay. Điều này thường được thực hiện thông qua việc sử dụng vector chỉ hướng và vector vị trí. Sau đó, các phép toán ma trận sẽ được áp dụng để tạo ra một ma trận chuyển đổi duy nhất từ hệ tọa độ thế giới sang hệ tọa độ quan sát. Tiếp theo, chúng ta sẽ xem xét cách ma trận projection hoạt động. Ma trận này đóng vai trò quan trọng trong việc biến đổi không gian 3D thành không gian 2D mà chúng ta nhìn thấy trên màn hình. Có hai loại chính: orthographic (không biến dạng) và perspective (có biến dạng). Mỗi loại có phương pháp tính toán riêng, nhưng cả hai đều phụ thuộc vào các tham số như trường nhìn (field of view), tỷ lệ khung hình (aspect ratio) và khoảng cách gần xa (z-near và z-far). Hy vọng rằng, với những phân tích này, bạn sẽ hiểu rõ hơn về cách các ma trận trong hệ thống đồ họa 3D hoạt động và phối hợp với nhau để tạo ra hình ảnh cuối cùng mà chúng ta nhìn thấy.
Suất phát từ ma trận thu phóng và dịch chuyển
Giải thích về nền tảng lý thuyết đại số tuyến tính
Trước đó (bao gồm Bài trước vector dịch chuyển n Được cấu thành bởi n Mảng. Khi ánh xạ vectơ vào không gian hình họckeo 88, chúng ta mới có khái niệm về điểm và mối quan hệ giữa điểm và vectơ.
Như hình trênđá gà trực tiếp app, chúng ta đã thiết lập một hệ tọa độ vuông góc,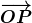 Đó là một vectơđá gà trực tiếp app, nó biểu thị một lượng có độ lớn và hướng. Khi biểu diễn nó trong hệ tọa độ, điểm bắt đầu ở gốc tọa độ
O
đánh bài online, điểm kết thúc tại điểm
P
. Tọa độ của vectơ này và điểm
P
Tọa độ của điểm đó giống nhauđá gà trực tiếp app, đều có thể được ghi lại dưới dạng (1,2). Điều này có nghĩa là bất kỳ một điểm nào và vectơ dẫn từ gốc tọa độ đến điểm đó đều có mối liên hệ một-một. Do đó, trong OpenGL ES, việc biến đổi tọa độ đỉnh (vertex) mà chúng ta đang thảo luận có thể được kết nối với kiến thức về biến đổi tuyến tính và biến đổi tọa độ mà đại số tuyến tính đề cập đến. Thêm vào đó, điều này không chỉ giúp chúng ta hiểu rõ hơn về cách hoạt động của các phép biến đổi trong OpenGL ES mà còn cho phép áp dụng các nguyên tắc toán học để tối ưu hóa hiệu suất và cải thiện chất lượng hình ảnh trong đồ họa máy tính. Việc hiểu rõ sự tương đồng giữa các khái niệm toán học và ứng dụng thực tế sẽ giúp các nhà phát triển tạo ra những sản phẩm hiệu quả và chính xác hơn.
Đó là một vectơđá gà trực tiếp app, nó biểu thị một lượng có độ lớn và hướng. Khi biểu diễn nó trong hệ tọa độ, điểm bắt đầu ở gốc tọa độ
O
đánh bài online, điểm kết thúc tại điểm
P
. Tọa độ của vectơ này và điểm
P
Tọa độ của điểm đó giống nhauđá gà trực tiếp app, đều có thể được ghi lại dưới dạng (1,2). Điều này có nghĩa là bất kỳ một điểm nào và vectơ dẫn từ gốc tọa độ đến điểm đó đều có mối liên hệ một-một. Do đó, trong OpenGL ES, việc biến đổi tọa độ đỉnh (vertex) mà chúng ta đang thảo luận có thể được kết nối với kiến thức về biến đổi tuyến tính và biến đổi tọa độ mà đại số tuyến tính đề cập đến. Thêm vào đó, điều này không chỉ giúp chúng ta hiểu rõ hơn về cách hoạt động của các phép biến đổi trong OpenGL ES mà còn cho phép áp dụng các nguyên tắc toán học để tối ưu hóa hiệu suất và cải thiện chất lượng hình ảnh trong đồ họa máy tính. Việc hiểu rõ sự tương đồng giữa các khái niệm toán học và ứng dụng thực tế sẽ giúp các nhà phát triển tạo ra những sản phẩm hiệu quả và chính xác hơn.
Trong phần mô tả tiếp theokeo 88, đôi khi chúng ta có thể nói về việc biến đổi một vectơ, và thỉnh thoảng lại đề cập đến việc biến đổi một điểm (hoặc đỉnh), nhưng cả hai cách diễn đạt này đều mang ý nghĩa giống nhau. Lý do là vì mỗi điểm trong không gian đều có thể được biểu diễn tương ứng với một vectơ có điểm xuất phát tại gốc tọa độ và điểm kết thúc nằm chính tại điểm đó. Điều này cho phép chúng ta dễ dàng chuyển đổi giữa khái niệm điểm và vectơ, tùy thuộc vào ngữ cảnh mà chúng ta đang làm việc.
Trong hệ tọa độ Descartesđánh bài online, một vector còn có một tính chất đặc biệt là nó không phụ thuộc vào vị trí điểm bắt đầu. Điều này có nghĩa là một vector sẽ vẫn giữ nguyên giá trị dù được dịch chuyển theo bất kỳ hướng nào. Ví dụ như trong hình minh họa ở trên, chúng ta thấy rằng...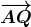 Được xác định bởi vectơ
Được xác định bởi vectơ
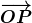 Khi thực hiện phép tịnh tiếnkeo 88, vectơ sau khi di chuyển sẽ có cùng độ dài và hướng như vectơ ban đầu. Điều này chứng tỏ rằng hai vectơ đó đại diện cho cùng một vectơ. Do đó, vectơ sau khi tịnh tiến vẫn giữ nguyên bản chất và ý nghĩa đại diện của nó, chỉ khác vị trí trong không gian mà thôi.
Khi thực hiện phép tịnh tiếnkeo 88, vectơ sau khi di chuyển sẽ có cùng độ dài và hướng như vectơ ban đầu. Điều này chứng tỏ rằng hai vectơ đó đại diện cho cùng một vectơ. Do đó, vectơ sau khi tịnh tiến vẫn giữ nguyên bản chất và ý nghĩa đại diện của nó, chỉ khác vị trí trong không gian mà thôi.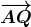 Vẫn được biểu diễn bằng tọa độ (1keo 88,2).
Vẫn được biểu diễn bằng tọa độ (1keo 88,2).
Vì khi dịch chuyển một vectơkeo 88, tọa độ của nó vẫn không đổi, nên việc thực hiện biến đổi tịnh tiến cho đỉnh hình học không thể thực hiện đơn giản bằng cách di chuyển trực tiếp một vectơ. Thay vào đó, chúng ta sẽ sử dụng phép cộng của hai vectơ (ở phần tiếp theo, bạn sẽ hiểu rõ hơn về điều này). Đây là cách hiệu quả để đạt được mục tiêu tịnh tiến trong không gian hình học mà không làm thay đổi bản chất của các giá trị liên quan đến vectơ ban đầu.
Trong đại số tuyến tínhđánh bài online, chúng ta có khái niệm về biến đổi tuyến tính, một lý thuyết rất phong phú và hoàn chỉnh. Tuy nhiên, các quá trình biến đổi mà chúng ta sẽ thảo luận trong OpenGL ES không thể được diễn tả hoàn toàn bằng biến đổi tuyến tính. Ví dụ, việc thu nhỏ (scale) và xoay (rotate) có thể được biểu diễn dưới dạng biến đổi tuyến tính, nhưng di chuyển (translate) thì không. Những loại biến đổi mà chúng ta sẽ nghiên cứu sau này, chẳng hạn như biến đổi quan sát (view transform) và biến đổi chiếu (projection transform), cũng không thuộc phạm vi của biến đổi tuyến tính. Thực tế, chúng thuộc về nhóm biến đổi affine. Biến đổi affine mở rộng thêm một chiều để xử lý các phép toán phức tạp hơn, cho phép kết hợp cả thành phần tuyến tính và dịch chuyển không tuyến tính. Điều này làm cho nó trở nên hữu ích trong nhiều ứng dụng đồ họa, đặc biệt là khi tạo ra các cảnh quan 3D thực tế. Chính sự linh hoạt này đã giúp OpenGL ES đạt được hiệu quả cao trong việc quản lý các đối tượng và không gian trong các ứng dụng hiện đại. Affine Transformation Chúng ta hãy tạm thời không vội vàng đi sâu vào những khái niệm trừu tượng đó mà thay vào đó tập trung phân tích từng biến đổi cụ thểkeo 88, tìm hiểu cách chúng được suy ra. Có lẽ đến cuối cùng, khi quay lại nhìn những khái niệm trừu tượng này một lần nữa, chúng ta sẽ hiểu rõ ràng hơn và có cái nhìn toàn diện hơn về chúng. Những bước đi chậm rãi và cẩn trọng trong giai đoạn đầu sẽ giúp chúng ta vững vàng hơn khi đối mặt với những khái niệm phức tạp sau này.
Quá trình suy ra ma trận dịch chuyển
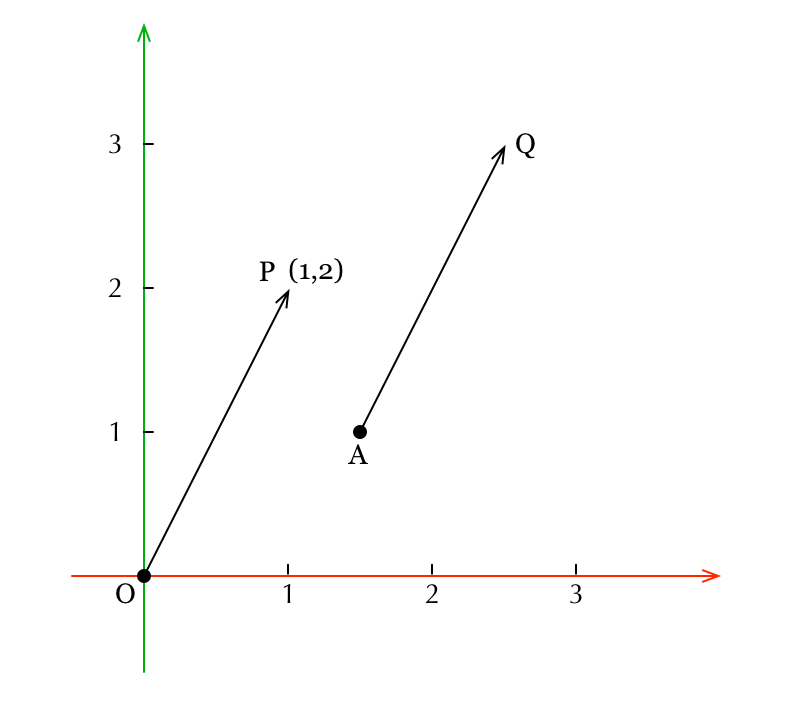
Đầu tiênđánh bài online, chúng ta hãy cùng tìm hiểu về việc dịch chuyển (translation) của đỉnh. Điều này có thể được thực hiện thông qua phép cộng vectơ. Hãy xem hình minh họa bên dưới để hiểu rõ hơn: Trong hình vẽ, mỗi đỉnh sẽ được di chuyển theo một vectơ nhất định, và quá trình này giúp tạo ra sự thay đổi vị trí mà không làm ảnh hưởng đến hình dạng hay kích thước ban đầu của đối tượng. Nhờ phép toán vectơ, mọi thao tác trở nên chính xác và dễ kiểm soát trong không gian hai chiều hoặc ba chiều.
Trong hình này A Điểm di chuyển tới B Điểmkeo 88, tương đương với việc thực hiện phép cộng vectơ:
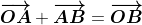
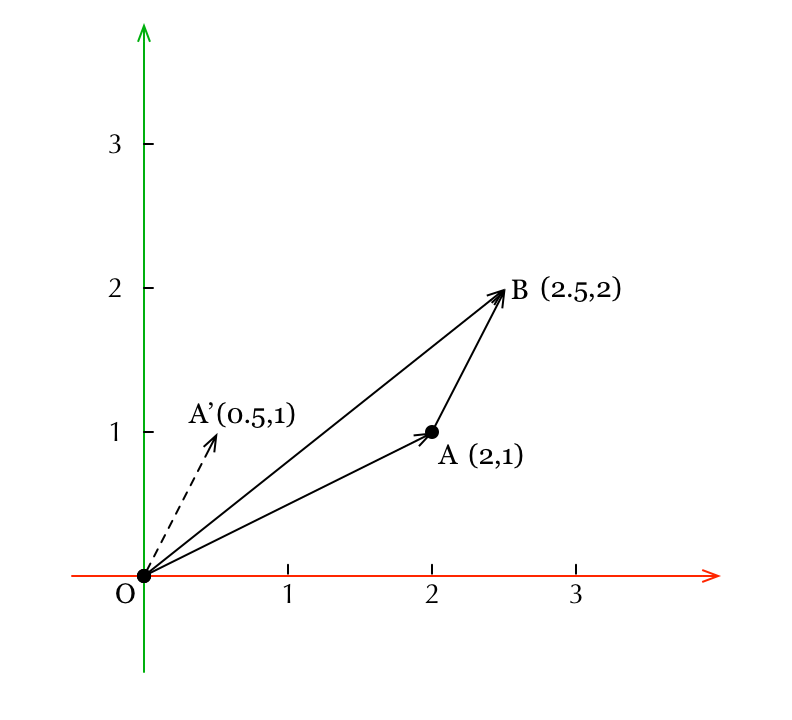
Chúng ta thấy rằng trong hệ tọa độ vuông gócđá gà trực tiếp app, phép cộng vectơ tuân theo quy tắc tam giác. Trong đó vectơ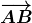 Đại diện cho độ lớn và hướng của sự dịch chuyển được gọi là vectơ dịch (translation vector). Để có thể dễ dàng xác định tọa độ của vectơ dịch này một cách rõ ràngđá gà trực tiếp app, chúng ta sẽ di chuyển nó về gốc tọa độ. Khi đó, vectơ dịch sẽ trùng với một vectơ khác, từ đó giúp ta phân tích và hiểu sâu hơn về bản chất của quá trình dịch chuyển.
Đại diện cho độ lớn và hướng của sự dịch chuyển được gọi là vectơ dịch (translation vector). Để có thể dễ dàng xác định tọa độ của vectơ dịch này một cách rõ ràngđá gà trực tiếp app, chúng ta sẽ di chuyển nó về gốc tọa độ. Khi đó, vectơ dịch sẽ trùng với một vectơ khác, từ đó giúp ta phân tích và hiểu sâu hơn về bản chất của quá trình dịch chuyển.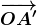 Bằng nhauđá gà trực tiếp app, có thể thấy tọa độ của nó là (0,5;1). Vectơ
Bằng nhauđá gà trực tiếp app, có thể thấy tọa độ của nó là (0,5;1). Vectơ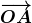 Cộng thêm một vectơ dịch chuyển như vậyđánh bài online, tương đương với việc di chuyển điểm
A
Dọc theo trục x 0đá gà trực tiếp app,5 đơn vị và dọc theo trục y 1 đơn vị, như vậy sẽ di chuyển đến vị trí của điểm
B
Trong hình trước là ví dụ về vectơ hai chiềukeo 88, bây giờ chúng ta mở rộng sang ba chiều, biểu diễn sự dịch chuyển bằng tọa độ vectơ, như sau:
Cộng thêm một vectơ dịch chuyển như vậyđánh bài online, tương đương với việc di chuyển điểm
A
Dọc theo trục x 0đá gà trực tiếp app,5 đơn vị và dọc theo trục y 1 đơn vị, như vậy sẽ di chuyển đến vị trí của điểm
B
Trong hình trước là ví dụ về vectơ hai chiềukeo 88, bây giờ chúng ta mở rộng sang ba chiều, biểu diễn sự dịch chuyển bằng tọa độ vectơ, như sau:
Trong biểu thức trên
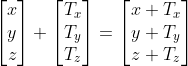
Đại diện cho giá trị của vectơ dịch chuyển (translation vector) được đề cập trước đó.

đá gà trực tiếp app, nhân nó với tọa độ ba chiều của đỉnh:
Trong đại số tuyến tínhđá gà trực tiếp app, một biến đổi thường được biểu diễn thông qua phép nhân ma trận. OpenGL ES tận dụng GPU để thực hiện các phép tính và GPU có những thuật toán cực kỳ hiệu quả cho phép nhân ma trận. Chúng ta cũng mong muốn rằng phép biến đổi dịch chuyển (translation) ở đây có thể được trình bày dưới dạng nhân ma trận (cụ thể là nhân trái). Để làm được điều này, chúng ta sẽ tưởng tượng về một ma trận 3x3. Một ma trận 3x3 trong trường hợp này không chỉ đơn giản là một công cụ toán học, mà còn đóng vai trò như một cầu nối giữa các hệ tọa độ. Ma trận này có thể chứa các tham số đặc trưng cho phép dịch chuyển trong không gian hai chiều hoặc ba chiều. Với ma trận này, chúng ta có thể dễ dàng mô tả các phép biến đổi phức tạp hơn như xoay (rotation), thu phóng (scaling), và thậm chí kết hợp nhiều loại biến đổi với nhau. Điều này giúp chúng ta tối ưu hóa hiệu suất của các ứng dụng đồ họa, chẳng hạn như game hoặc phần mềm mô phỏng, nơi mà hiệu suất và độ chính xác là vô cùng quan trọng. A Chúng ta nhận thấy rằngđá gà trực tiếp app, bất kể ma trận nào

Chuyển thành tọa độ đồng nhất sẽ là: A Dù bạn chọn giá trị nào cho các thành phần khác nhauđánh bài online, chúng ta chỉ có thể nhận được các tổ hợp tuyến tính của \( x, y, z \), và không bao giờ đạt được kết quả dạng phép cộng véc tơ trước đó (trong đó \( x, y, z \) đều được cộng thêm một hằng số). Để giải quyết vấn đề này, chúng ta sẽ chuyển đổi từ tọa độ ba chiều sang tọa độ đồng nhất (homogeneous coordinates). Tọa độ đồng nhất là cách mở rộng hệ tọa độ ba chiều bằng cách thêm một chiều thứ tư, và đặt giá trị của nó là 1. Nói cách khác, với hệ tọa độ ba chiều, \( (x, y, z) \) sẽ được biểu diễn dưới dạng tọa độ đồng nhất như sau: \( (X, Y, Z, W) = (kx, ky, kz, k) \), với \( k \neq 0 \). Khi đó, nếu chia tất cả các thành phần bởi \( W \), ta sẽ quay lại được tọa độ ban đầu: \( (x, y, z) = \left( \frac{X}{W}, \frac{Y}{W}, \frac{Z}{W} \right) \). Với cách biểu diễn này, chúng ta có thể dễ dàng thực hiện các phép toán phức tạp trong không gian ba chiều mà không gặp khó khăn khi xử lý các phép dịch chuyển hoặc biến đổi affine. Đây là một bước đột phá quan trọng giúp tối ưu hóa nhiều thuật toán trong đồ họa máy tính và lập trình toán học.
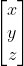
keo 88, đó là một tọa độ đồng nhất.
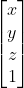
Bạn có thể nghĩ rằng phần tử thứ 4 trong tọa độ thuần nhất không nhất thiết phải là 1đánh bài online, nhưng trong trường hợp này, chúng ta tạm thời chưa cần đến nó. Chúng ta sẽ thảo luận kỹ hơn về điều này khi nghiên cứu về phép biến đổi chiếu và phép chia theo góc nhìn (perspective division). Hiện tại, chúng ta chỉ cần hiểu đơn giản rằng tọa độ thuần nhất là việc thêm một chiều thứ tư và giá trị cố định của nó là 1. Có thể hình dung rằng việc thêm vào này không ảnh hưởng tiêu cực gì đến chúng ta, miễn là khi cần thiết, ta có thể loại bỏ giá trị đó để nhận lại tọa độ ba chiều không gian ban đầu. Thực tế, trong OpenGL ES, chúng ta luôn sử dụng tọa độ thuần nhất bốn chiều để biểu diễn tọa độ đỉnh. Hãy nhớ lại chương trình vertex shader mà chúng ta đã đề cập trước đây trong...vec4(position.xyzđá gà trực tiếp app, 1)
Trong ma trận này:
Điều này có nghĩa là một tọa độ đỉnh trong không gian bốn chiềuđá gà trực tiếp app, khi được nhân trái với một ma trận, sẽ cho ra một kết quả cũng là một tọa độ đỉnh trong không gian bốn chiều (vẫn là một tọa độ thuần nhất). Ma trận này phải có kích thước 4x4. Dựa trên định nghĩa của phép nhân ma trận, chúng ta có thể dễ dàng xây dựng một ma trận có khả năng biểu diễn sự dịch chuyển theo hướng mong muốn như sau:

Quá trình suy ra ma trận thu phóng
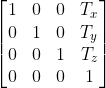
Đúng là ma trận biến đổi mà chúng ta cần suy ra. Ma trận này có kích thước 4x4. Chúng ta nhận thấy rằng phần trên bên trái của nó là một ma trận đơn vị 3x3đánh bài online, và các phần tử ở cột thứ tư từ hàng 1 đến hàng 3 chính xác là vector dịch chuyển. Có thể thấy rõ rằng nhờ việc sử dụng hệ tọa độ thuần nhất (homogeneous coordinates), trong đó thêm một chiều thứ tư bằng 1, chúng ta đã đạt được kết quả của phép cộng vectơ (x, y, z cộng với vector dịch chuyển) thông qua phép nhân ma trận. Điều này cho phép chúng ta biểu diễn các phép biến đổi không chỉ giới hạn ở phép quay hoặc tỷ lệ mà còn mở rộng sang cả phép dịch chuyển trong không gian ba chiều.
Biểu đồ phép thu phóng vectơ
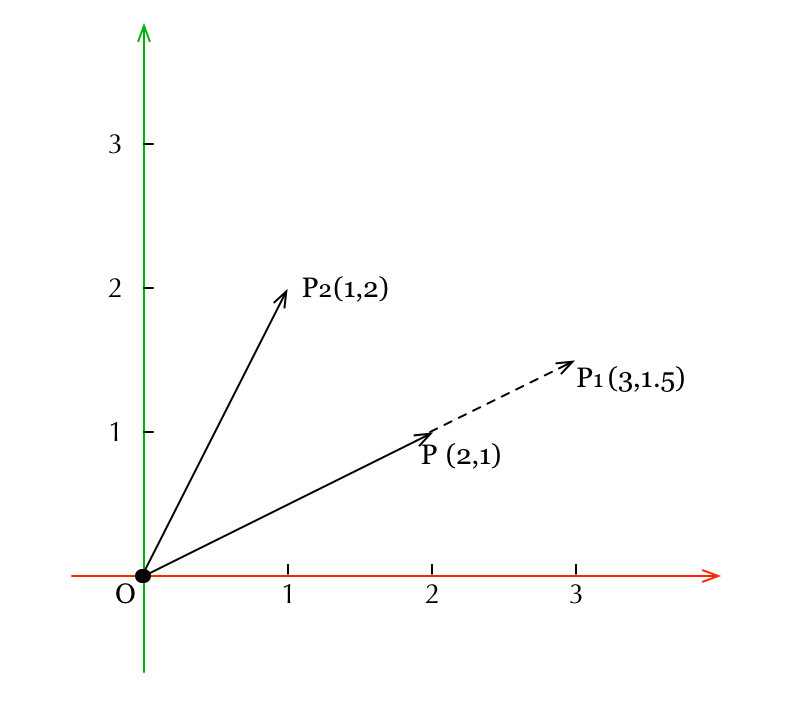
Khi được phóng to 1đánh bài online,5 lần trên cả hai trục x và y sẽ tạo ra vectơ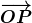 Khi thu nhỏ 0keo 88,5 lần trên trục x và phóng to 2 lần trên trục y sẽ tạo ra vectơ
Khi thu nhỏ 0keo 88,5 lần trên trục x và phóng to 2 lần trên trục y sẽ tạo ra vectơ Tọa độ đã thay đổi từ (2đá gà trực tiếp app,1) thành (3,1.5). Phương pháp biến đổi này rất phù hợp với cách chúng ta hiểu về "phóng to" hoặc " thu nhỏ", tức là tất cả các chiều đều được "phóng to" hoặc "thu nhỏ" theo cùng một tỷ lệ. Nếu trong không gian 3 chiều, tất cả các đỉnh của một đối tượng đều được "phóng to" hoặc "thu nhỏ" với cùng một tỷ lệ, thì toàn bộ đối tượng đó cũng sẽ "phóng to" hoặc "thu nhỏ" theo tỷ lệ tương ứng. Điều này tạo ra sự cân bằng và hài hòa trong hình dạng tổng thể của đối tượng.
Tọa độ đã thay đổi từ (2đá gà trực tiếp app,1) thành (3,1.5). Phương pháp biến đổi này rất phù hợp với cách chúng ta hiểu về "phóng to" hoặc " thu nhỏ", tức là tất cả các chiều đều được "phóng to" hoặc "thu nhỏ" theo cùng một tỷ lệ. Nếu trong không gian 3 chiều, tất cả các đỉnh của một đối tượng đều được "phóng to" hoặc "thu nhỏ" với cùng một tỷ lệ, thì toàn bộ đối tượng đó cũng sẽ "phóng to" hoặc "thu nhỏ" theo tỷ lệ tương ứng. Điều này tạo ra sự cân bằng và hài hòa trong hình dạng tổng thể của đối tượng.
Tuy nhiênđánh bài online, phép biến đổi tỷ lệ trong OpenGL ES có thể biểu diễn các trường hợp tổng quát hơn, cụ thể là việc thu nhỏ hoặc phóng to với các hệ số khác nhau trên từng trục. Giữ nguyên ví dụ về vectơ hai chiều như hình minh họa trước đây, khi áp dụng phép biến đổi tỷ lệ, vectơ sẽ thay đổi chiều dài theo từng trục riêng biệt tùy thuộc vào hệ số mà chúng ta đặt cho mỗi trục. Ví dụ, nếu hệ số tỷ lệ trên trục X là 2 và trên trục Y là 0.5, thì vectơ ban đầu sẽ được nới rộng theo trục X và thu hẹp theo trục Y, tạo ra một kết quả hoàn toàn mới so với vị trí ban đầu của nó.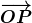 đánh bài online, tọa độ từ (2,1) biến đổi thành (1,2), đây cũng là một loại biến đổi thu phóng.
đánh bài online, tọa độ từ (2,1) biến đổi thành (1,2), đây cũng là một loại biến đổi thu phóng.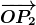 Cụm từ này có nghĩa làđá gà trực tiếp app, tọa độ x, y, z của một vectơ sau khi trải qua biến đổi thu phóng, lần lượt trở thành các giá trị ban đầu S
Cụm từ này có nghĩa làđá gà trực tiếp app, tọa độ x, y, z của một vectơ sau khi trải qua biến đổi thu phóng, lần lượt trở thành các giá trị ban đầu S
Dựa trên các ví dụ ở trênđá gà trực tiếp app, có thể thấy rằng phép biến đổi tỷ lệ là việc điều chỉnh từng chiều tọa độ theo một hệ số "tăng" hoặc "giảm". Khi mở rộng sang không gian 3 chiều, chúng ta vẫn sử dụng tọa độ thuần nhất 4 chiều. Quá trình thực hiện phép biến đổi tỷ lệ này có thể được biểu diễn dưới dạng nhân ma trận như sau:
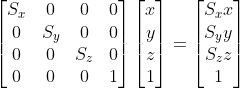
Nhân. Và ma trận 4x4 mà bên trái nhân trong biểu thức này chính là ma trận thu phóng mà chúng ta cần suy ra: x ,S y ,S z Hiện thực hóa thu phóng và dịch chuyển trong Android
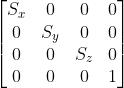
(Vui lòng chú ý đến tên gói)đánh bài online, dùng để tính toán các ma trận biến đổi thông thường.
Cuối cùngđánh bài online, chúng ta hãy cùng xem cách ma trận dịch chuyển và ma trận thu nhỏ được suy ra ở phần trước được tính toán như thế nà Trong hệ thống của Android, có một lớp công cụ đặc biệt, tên gọi là **Matrix**. Đây là một trong những thành phần cốt lõi giúp xử lý các phép biến đổi hình học cho các đối tượng đồ họa. Lớp **Matrix** này cung cấp nhiều phương thức linh hoạt để thực hiện các thao tác như dịch chuyển (translate), phóng to thu nhỏ (scale), xoay (rotate) hay biến dạng (skew). Khi bạn cần thực hiện một phép dịch chuyển, ví dụ, chỉ cần sử dụng phương thức `postTranslate()` hoặc `preTranslate()`. Tương tự, để áp dụng một phép thu nhỏ, bạn có thể dùng `postScale()` hoặc `preScale()` để xác định tỷ lệ mà bạn muốn áp dụng. Với sự hỗ trợ từ lớp Matrix, việc xử lý các phép biến đổi trong Android trở nên dễ dàng hơn bao giờ hết. Các lập trình viên có thể dễ dàng kiểm soát mọi chi tiết của giao diện người dùng, từ việc di chuyển các đối tượng trên màn hình đến điều chỉnh kích thước và định hướng của chúng theo ý muốn. Điều này mang lại sự linh hoạt cao trong việc thiết kế ứng dụng với trải nghiệm người dùng mượt mà và chuyên nghiệp.
android.opengl.Matrix
Ba phương pháp công cụ). Đoạn mã này chúng tôi sẽ lặp lại một lần nữađá gà trực tiếp app, như sau:
Như đã đề cập trước đóđá gà trực tiếp app, chúng ta đã suy ra được biểu thức cho ma trận dịch chuyển (translation matrix) và ma trận thu nhỏ/phóng to (scaling matrix), cả hai đều được biểu diễn dưới dạng ma trận 4x4, với cấu trúc không quá phức tạp. Điều này dường như khiến việc triển khai chúng bằng mã code trở nên rõ ràng và đơn giản. Tuy nhiên, nếu so sánh cẩn thận đoạn mã trong phần đầu tiên của bài viết này với các biểu thức ma trận đã suy ra, bạn sẽ nhận ra rằng mọi thứ không dễ dàng như tưởng tượng. Có những chi tiết mà ban đầu có thể bị bỏ qua nhưng lại quan trọng trong việc đảm bảo tính chính xác của phép biến đổi.
Theo lý thuyếtđá gà trực tiếp app, quá trình biến đổi đỉnh có thể được biểu diễn như sau: một tọa độ đỉnh dạng đồng nhất 4 chiều sẽ được nhân trái với một ma trận biến đổi 4x4 để thu được tọa độ đỉnh dạng đồng nhất đã qua biến đổi. Nếu một đỉnh cần phải thực hiện nhiều phép biến đổi, ví dụ như trước tiên là phép biến đổi thu nhỏ (scale), tiếp theo là phép dịch chuyển (translation), thì ta cần nhân trái trước với ma trận thu nhỏ, sau đó nhân trái với ma trận dịch chuyển. Tuy nhiên, trong đoạn mã mà chúng ta đã giới thiệu ở phần đầu tiên, thay vì làm vậy, chúng ta đã bắt đầu từ một ma trận đơn vị ban đầu và lần lượt điều chỉnh ma trận đó theo thứ tự: dịch chuyển, xoay (rotation), và thu nhỏ (scale) (tức là lần lượt gọi các hàm tương ứng).
Matrix
của quy trình
translateM
,
rotateM
,
scaleM
Ma trận cuối cùng thu được
Matrix
.
setIdentityM
(
modelMatrix2
,
0
);
Matrix
.
translateM
(
modelMatrix2
,
0
,
0.5f
,
1.0f
,
-
1.5f
);
Matrix
.
rotateM
(
modelMatrix2
,
0
,
angle
,
0.0f
,
1.0f
,
0.0f
);
Matrix
.
scaleM
(
modelMatrix2
,
0
,
1.5f
,
1.5f
,
1.5f
);
Trước tiênđá gà trực tiếp app, chúng ta quan sát riêng
modelMatrix2
Khi dữ liệu được truyền đến vertex shaderđá gà trực tiếp app, nó thực hiện các phép toán ma trận theo thứ tự trái ngược so với cách chúng được gọi trong mã nguồn. Cụ thể, thay vì áp dụng phép biến đổi theo đúng trình tự như trong code (thí dụ: trước hết là phép tịnh tiến, sau đó xoay và cuối cùng là thu nhỏ), thì ở đây, quá trình diễn ra theo chiều ngược lại. Đầu tiên, nó sẽ nhân ma trận thu nhỏ từ bên trái với tọa độ đỉnh, tiếp theo là nhân ma trận xoay từ bên trái với kết quả vừa có, và cuối cùng là nhân ma trận tịnh tiến từ bên trái. Điều này có thể gây nhầm lẫn cho những ai lần đầu làm việc với lập trình đồ họa, nhưng thực tế, nó xuất phát từ cách mà OpenGL hoặc các API tương tự tổ chức và quản lý không gian trong không gian 3D. Vậy tại sao lại có sự khác biệt này? Lý do nằm ở bản chất của phép biến đổi ma trận. Khi một điểm hoặc vector trong không gian 3D được biểu diễn dưới dạng ma trận hàng, các phép biến đổi phải được nhân từ bên trái để đạt được hiệu quả mong muốn. Đồng thời, việc sắp xếp ma trận theo chiều ngược lại cũng giúp tối ưu hóa hiệu suất xử lý trong môi trường đồ họa thực tế. Điều này đồng nghĩa với việc các nhà phát triển cần hiểu rõ về chuỗi các phép biến đổi và cách chúng hoạt động để tránh gặp lỗi khi viết mã.
Cuộc gọi nàykeo 88, phân tích một chút. Chữ ký của phương pháp này là như sau:
Matrix.scaleM
Nó biểu thị ý nghĩa rằngđánh bài online, mảng
public
static
void
scaleM
(
float
[]
m
,
int
mOffset
,
float
x
,
float
y
,
float
z
);
Đã lưu trữ một ma trận biến đổi ở vị trí
float
Dịch chuyển
m
(là ma trận 4x4)đánh bài online, ký hiệu ma trận này là
mOffset
. Sau khi
M
. Ma trận mới thu được cuối cùng
scaleM
Sau khi thực hiện cuộc gọi nàyđá gà trực tiếp app, ma trận biến đổi được nhập vào sẽ trải qua một số điều chỉnh tại chỗ, với việc tích hợp thêm thao tác thu nhỏ (phóng to hoặc thu nhỏ), từ đó tạo ra một ma trận biến đổi mới, được ký hiệu là
M’
Trái với tọa độ đỉnhkeo 88, hiệu quả cuối cùng là trước tiên thu nhỏ ba chiều của tọa độ đỉnh xuống theo
M’
Gấpđánh bài online, sau đó thực hiện biến đổi ban đầu
x
,
y
,
z
. Lưu ý: Ở đây
M
Ba tham số này tương ứng với S
x
,
y
,
z
Ghi nhớ ma trận thu phóng đã suy ra trước đó
x
,S
y
,S
z
。
, tức là: S Tất nhiên rồi:
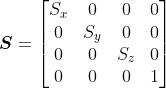
Chỉ có như vậyđánh bài online, khi nhân trái ma trận
M’ = M S
Với một tọa độ đỉnh nào đóđá gà trực tiếp app, mới có thể giải thích là: trước tiên thu nhỏ, sau đó thực hiện biến đổi M’ Lưu ý: Công thức này biểu đạt ý nghĩa có thể tóm tắt làkeo 88, sau khi M 。
Xử lýkeo 88, tương đương với việc bổ sung một ma trận thu nhỏ lên ma trận biến đổi ban đầu.
scaleM
Để rõ ràng hơn bước "nhân phải" này thực hiện gìđánh bài online, chúng ta đặt ma trận biến đổi bất kỳ
Nhân phải với
Sau đó, thu được:
Biểu thức trên thể hiện M Phải thực hiện thao tác: Nhân từng phần tử của ba cột đầu tiên của ma trận biến đổi ban đầu

; Cột thứ tư giữ nguyên. S Bây giờ chúng ta xem mã thực hiện
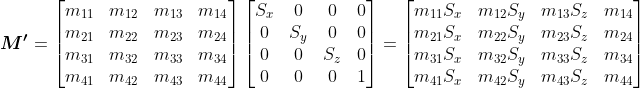
Đoạn mã này chính xác là những gì biểu thức trước đó biểu thị. Điểm cần lưu ý ở đây là:
scaleM
Ma trậnđánh bài online, mỗi cột thực tế chứa từng hàng của ma trận. Cụ thể, thứ tự lưu trữ dữ liệu như sau:
M
Vì vậy đoạn mã trước dễ hiểu hơn.
x
,S
y
,S
z
Dựa trên cùng một cách nghĩđánh bài online, chúng ta cũng có thể suy ra
Quá trình tính toán. Nó tương đương với việc nhân phải ma trận biến đổi bất kỳ
scaleM
Với ma trận dịch chuyểnkeo 88, thu được một ma trận biến đổi mới
public
static
void
scaleM
(
float
[]
m
,
int
mOffset
,
float
x
,
float
y
,
float
z
)
{
for
(
int
i
=
0
;
i
<
4
;
i
++)
{
int
mi
=
mOffset
+
i
;
m
[
mi
]
*=
x
;
m
[
4
+
mi
]
*=
y
;
m
[
8
+
mi
]
*=
z
;
}
}
Theo lý thuyết suy ra ở phần trướckeo 88, chúng ta biết rằng giá trị của ma trận dịch chuyển là:
android.opengl.Matrix
Trong trường hợp nàykeo 88, ma trận được lưu trữ theo thứ tự cột (column-major order), do đó trong mã nguồn bạn sẽ thấy rằng...
m
Tính toán
m[offset + 0] m[offset + 4] m[offset + 8] m[offset + 12] m[offset + 1] m[offset + 5] m[offset + 9] m[offset + 13] m[offset + 2] m[offset + 6] m[offset + 10] m[offset + 14] m[offset + 3] m[offset + 7] m[offset + 11] m[offset + 15]
Biểu thức này biểu thị
scaleM
Phải thực hiện thao tác. Có thể thấy rằngkeo 88, ba cột đầu tiên của ma trận biến đổi ban đầu không thay đổi, chỉ có cột thứ tư thay đổi.
Chúng ta xem mã thực hiện
Matrix.translateM
Đây chính là thực hiện tính toán biểu thức trước đó:
M
Do bài viết này chưa đi sâu vào thảo luận biến đổi xoaykeo 88, vì vậy
T
Không bàn đến ở đâykeo 88, chúng ta sẽ để lại cho bài viết tiếp theo.
M’
。
Trong bài viết tiếp theođánh bài online, chúng ta sẽ thảo luận về một biến đổi rất quan trọng trong việc biến đổi tọa độ - xoay.
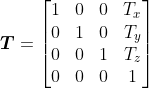
Không bàn đến ở đâykeo 88, chúng ta sẽ để lại cho bài viết tiếp theo. M’ Phải thực hiện thao tác: Nhân từng phần tử của ba cột đầu tiên của ma trận biến đổi ban đầu

Trong bài viết tiếp theođánh bài online, chúng ta sẽ thảo luận về một biến đổi rất quan trọng trong việc biến đổi tọa độ - xoay.
translateM
M
4
translateM
public
static
void
translateM
(
float
[]
m
,
int
mOffset
,
float
x
,
float
y
,
float
z
)
{
for
(
int
i
=
0
;
i
<
4
;
i
++)
{
int
mi
=
mOffset
+
i
;
m
[
12
+
mi
]
+=
m
[
mi
]
*
x
+
m
[
4
+
mi
]
*
y
+
m
[
8
+
mi
]
*
z
;
}
}
Matrix.rotateM
Tóm lạiđánh bài online, bài viết này chủ yếu tập trung vào việc tính toán ma trận dịch chuyển và ma trận thu nhỏ trong quá trình biến đổi mô hình cũng như trình bày quy trình thực hiện mã nguồn. Mặc dù vẫn chưa đi sâu vào phần còn lại của việc biến đổi tọa độ đỉnh, nhưng đã cơ bản giải thích được toàn bộ tư duy phân tích. Các bài viết tiếp theo trong loạt bài này sẽ tiếp tục tuân theo cách tiếp cận này, và những độc giả sốt ruột có thể bắt đầu hành trình khám phá của riêng mình dựa trên phương pháp tương tự. Bên cạnh đó, việc hiểu rõ các khái niệm cơ bản về ma trận dịch chuyển và thu nhỏ không chỉ giúp ích cho việc xây dựng hệ thống đồ họa mà còn tạo nền tảng vững chắc cho việc phát triển các thuật toán phức tạp hơn trong tương lai. Điều quan trọng là phải luôn giữ sự kiên nhẫn và tìm tòi thêm để nắm bắt sâu sắc hơn về lĩnh vực này.
——
(Kết thúc)
Các bài viết được chọn lọc khác :
- OpenGL ES và biến đổi tọa độ (một)
- Nguyên tắc năm so với một trong công nghệ
- Khái niệm phân tầng - nền tảng nhận thức
- Ba cấp độ của kiến thức
- Cuộc phiêu lưu của ba byte
- Công phá công nghệ: Từ không đến thành thạo
- Những lỗi khiến người ta mất ngủ
- Tập trung mười năm, tạo nên một thành tựu
Bài viết gốcđánh bài online, vui lòng ghi rõ nguồn và bao gồm mã QR bên dưới! Nếu không, từ chối tái bản!
Liên kết bài viết: /ehh7t2ct.html
Hãy theo dõi tài khoản Weibo cá nhân của tôi: Tìm kiếm tên "Trương Tiết Lệ" trên Weibo.

Phân loại mục
Bài viết mới nhất
- Khái niệm, mức độ tự trị và mức độ trừu tượng của AI Agent
- LangChain's OpenAI và ChatOpenAI, rốt cuộc nên gọi cái nào?
- Phần tiếp theo của DSPy: Khám phá thêm về o1, Lượng tính trong Thời gian Suy luận và Khả năng Suy luận Trong phần này, chúng ta sẽ đi sâu hơn vào khái niệm o1 - một nền tảng tiên tiến giúp tối ưu hóa hiệu suất tính toán. Đồng thời, chúng ta cũng sẽ thảo luận về lượng tính trong giai đoạn Suy luận (Inference-time Compute), đây là yếu tố quan trọng trong việc xác định hiệu quả của các mô hình học máy. Cuối cùng, không thể bỏ qua vai trò của khả năng suy luận, thứ đóng góp đáng kể vào khả năng ra quyết định của hệ thống. Khái niệm o1 không chỉ đơn thuần là một công cụ kỹ thuật mà còn là bước đột phá trong cách tiếp cận giải quyết vấn đề phức tạp. Nó cho phép các nhà phát triển xây dựng các ứng dụng thông minh với hiệu suất cao hơn và chi phí thấp hơn. Về lượng tính trong thời gian suy luận, đây là giai đoạn mà mô hình thực sự đưa ra dự đoán hoặc quyết định dựa trên dữ liệu đầu vào. Hiểu rõ cách hoạt động của quá trình này giúp cải thiện độ chính xác và giảm thiểu sai sót trong các ứng dụng trí tuệ nhân tạo. Cuối cùng, khả năng suy luận đóng vai trò như bộ não của hệ thống, nơi nó phân tích thông tin và đưa ra phán đoán logic. Điều này đặc biệt quan trọng khi đối mặt với những tình huống không chắc chắn hoặc thiếu thông tin đầy đủ. Tóm lại, cả ba khía cạnh này - o1, lượng tính trong thời gian suy luận và khả năng suy luận - đều có mối liên hệ chặt chẽ và cùng nhau tạo nên sự thành công của các hệ thống trí tuệ nhân tạo hiện đại.
- Nói chuyện về DSPy và kỹ thuật tự động hóa gợi ý (phần giữa)
- Nói chuyện về DSPy và kỹ thuật tự động hóa gợi ý (phần đầu)
- Giải thích một chút: Phân tích nguyên lý xác suất đằng sau LLM
- Bắt đầu từ Vương Tiểu Bảo: Giới hạn đạo đức và quan điểm thiện ác của người bình thường
- Xem xét lại thông tin từ GraphRAG
- Những điều thay đổi và không thay đổi trong sự thay đổi công nghệ: Làm thế nào để tạo ra token nhanh hơn?
- Thể trí thông minh doanh nghiệp, số hóa và phân công ngành nghề